Licence: Public Domain Mark
Credit: Die Idee der Riemannschen Fläche. Source: Wellcome Collection.
Provider: This material has been provided by the Gerstein Science Information Centre at the University of Toronto, through the Medical Heritage Library. The original may be consulted at the Gerstein Science Information Centre, University of Toronto.
60/196 (page 44)
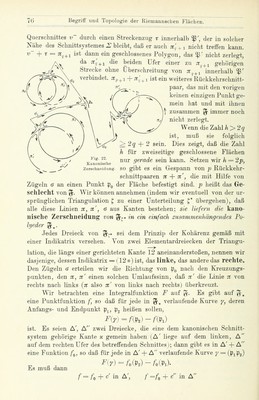
![das eine der beiden Enden der Elementarstrecke als Anfangspunkt, das andere als Endpunkt bezeichnet wird, ist diese Strecke gerichtet. Endlich- viele Elementarstrecken <?i (Jg • • G„ bilden einen Streckenzug, wenn immer der Endpunkt von 6,^ mit dem Anfangspunkt von ö^^^ [h=l,2, ••, n—1] zusammenfällt. Haben irgend zwei Strecken eines Streckenzuges nur dann, wenn sie aufeinander folgen, einen (und auch nur einen) Punkt gemein, so iiberschiieidet sieh der Streckenzug nicht: er ist ein „ein- facher'^ Streckenzug. Stimmt der Endpunkt von 6^ mit dem Anfangs- punkt von 6^ überein, so ist der Streckenzug geschlossen; 6^ ist dann die auf (?^ folgende Strecke (zyklische Anordnung). Ein geschlossener Streckenzug, in dem zwei Strecken nur dann einen Punkt gemein haben, wenn sie aufeinanderfolgen, wird als Polygon bezeichnet. Zuei Punkte eines Gehieis (5} avf '^^ lassen sich stets durch einen einfachen StrecTienzug verbinden, der ganz in @ terläufi. Man kann näm- lich die beiden Punkte zunächst durch eine ganz in @ verlaufende Kurve y verbinden. Von der Einteilung t, kann man eine so feine Unterteilung l' herstellen, daß alle Elementardreiecke von t', welche Punkte mit y gemein haben, in @ liegen. Durch die auf S. 23 f. angegebene Konstruktion erhält man eine einfache Kette von Dreiecken der Einteilung t,', welche dasjenige Dreieck von t,', in dem der Anfangspunkt von y liegt, mit dem den Endpunkt von y enthaltenden Dreieck verbindet. Die Dreieckskette läßt sich dann sofort durch einen einfachen Streckenzug ersetzen, der die Dreiecke der Kette sukzessive in je einer Strecke durchquert. — Femer: Ist 6 irgend ein Streckenzug auf %;-, so kann man eine solche Unter- teilung l' von l angeben, daß die Strecken, aus denen 6 besteht, Kanten der Teilung t,' (oder aus Kanten von t,' zusammengesetzt) sind, daß also 6 auf %■-■ ein Kantenzug ist. Von einer abgeschlossenen Menge © auf ^ sagen wir, sie zerlegt % nicht, wenn die Punkte von %, die Fig. 10. Einfacher streokenzug mit nicht ZU (S gehören, ein einziges Ge- anstoflenden Dreiecken. \^^q^ ausmacheu. Ein einfacher Strecken- zug G zerlegt %r nickt. Wir machen zum Beweise eine solche Untertei- lung ^' von t„ daß 6 als Kantenzug erscheint. Die an 6 anstoßendem Dreiecke von t,' lassen sich dann in solcher Weise durchnumerieren: 1,. 2, 3, . . ., daß je zwei aufeinanderfolgende Dreiecke in dieser Numerie- rung eine nicht zu 6 gehörige Kante gemein haben. Durch die Figur ist der Beginn einer solchen Numerierung angedeutet^). Ich behaupte,, daß irgend zwei Punkte p und q von % miteinander durch eine stetige^ 6 nicht treffende Kurve verbunden werden können. Ich verbinde p und 1) Man wird dabei freilich nicht immer vermeiden können, daß dasselbe Dreieck gelegentlich zwei- oder mehrmals mit verschiedenen Nummern auftritt.](https://iiif.wellcomecollection.org/image/b20996469_0060.jp2/full/800%2C/0/default.jpg)