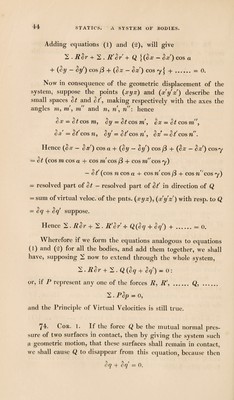The mathematical principles of mechanical philosophy, and their application to elementary mechanics and architecture, but chiefly to the theory of universal gravitation / [John Henry Pratt].
- Pratt, John H. (John Henry), 1809-1871.
- Date:
- 1842
Licence: Public Domain Mark
Credit: The mathematical principles of mechanical philosophy, and their application to elementary mechanics and architecture, but chiefly to the theory of universal gravitation / [John Henry Pratt]. Source: Wellcome Collection.
79/670 page 39
![THE EQUILIBRIUM OF A SYSTEM OF RIGID BODIES. 68. In order to obtain the conditions of equilibrium of two or more rigid bodies connected together in any way what¬ ever, we must substitute unknown forces in the place of the mutual actions at the points of connexion, and then write down the equations of equilibrium of each body. These systems of equations will be connected together, since a force depending on the mutual actions of any two of the bodies must enter both the systems of equations, which correspond to those bodies. Prop. To find the conditions of equilibrium of a system of bodies acted on by given forces. 69. Let any one of the bodies A be acted on by the given forces X{YfZx, . at the points . also suppose that in consequence of the connexion of the system a mutual force P acts between the bodies A and 1?, making angles afiy with the axes: and let ay/y/a?/ be its point of application in A, and xfiy^x^ the point of application in B. Now if we suppose the force P to act on A and analogous forces for all the other mutual actions arising from the con¬ nexion of the system, the body A may be supposed to be in equilibrium under the action of these forces and the forces XlYiZl .. Hence by Art. 56, 2 . Xl + P cos a +.=0, 2 . F] + P cos /3 -f.=0, 2 • Z\ ■+■ P cos ry~}- ...... — 0, 2. (Z\y\ - Pi#i) + P (y/ cos y - cos /3) +.= o, 2 . (X1z1 — Zxx^) + P (#/ cos a — Wj cos y) +.=0, 2. (Fi&’i — Xx ij\) + P (,r/ cos — yl cos a) + , = 0.](https://iiif.wellcomecollection.org/image/b29286700_0079.jp2/full/800%2C/0/default.jpg)