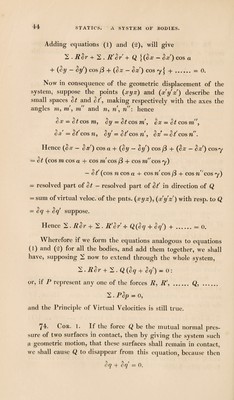The mathematical principles of mechanical philosophy, and their application to elementary mechanics and architecture, but chiefly to the theory of universal gravitation / [John Henry Pratt].
- Pratt, John H. (John Henry), 1809-1871.
- Date:
- 1842
Licence: Public Domain Mark
Credit: The mathematical principles of mechanical philosophy, and their application to elementary mechanics and architecture, but chiefly to the theory of universal gravitation / [John Henry Pratt]. Source: Wellcome Collection.
82/670 page 42
![a rigid body, be as well accomplished by supposing the co¬ ordinate axes to receive a slight alteration of position. Suppose the axes to revolve round z through a small angle 0: then oo, y, z become at + yO, y - atO, z, neglecting small quantities of the second and higher orders. Next, suppose these new axes to revolve through a small angle (p about the new axis of y: by these means the original values at, y, % become (at + y6)-Z(p, y-)VQ, z+(xt+y6)(p, or at + y6-z<p> y - atO, z + at(p. Next, suppose the axes to revolve about the new axis of at, through a small angle \fr, and the co-ordinates become at + yO-zcp, y - atO + z\js, z + at(p-y\]s, omitting small quantities of the second and higher orders. Lastly, let the origin be shifted to a point whose co-ordi¬ nates are a, b, c: hence, if Sat, Sy, Sz be the total changes in at, y, ss produced by these changes of axes, Sat = a + y6 - zcp.(l), Sy = b + z\js - atO . (2), Sz = c + at(p - y\js.(3). Now multiply the equations of equilibrium 2 . X = o, 2. Y = 0, 2. Z = o, 2 • (Xy — Yat) = 0, 2 . (Zat - Xz) = 0, 2.(Yz - Zy) = 0, by a, b, c, 0, (p, \Js respectively, and add; .*.2.{ + + Y(b + z\p~atO) + Z(c + .r0-y^)} = 0; and, consequently, 2. {^rS®+ YSy + ZSz} « o.](https://iiif.wellcomecollection.org/image/b29286700_0082.jp2/full/800%2C/0/default.jpg)