Copy 1

Mechanick powers; or, The mystery of nature and art unvail'd ... Together, with a treatise of circular motion artificially fitted to mechanick use, and the making of clock-work, and other engines ... The whole comprized in ten books, and illustrated with copper cuts / By Ven. Mandey Philomat [and J. Moxon].

Venterus Mandey

Date:: 1709

Credit: Mechanick powers; or, The mystery of nature and art unvail'd ... Together, with a treatise of circular motion artificially fitted to mechanick use, and the making of clock-work, and other engines ... The whole comprized in ten books, and illustrated with copper cuts / By Ven. Mandey Philomat [and J. Moxon]. Source: Wellcome Collection.

322/378 page 280

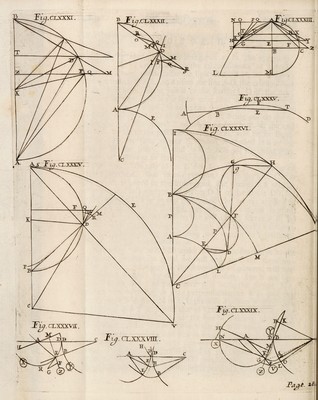
$PRO P 0 S. II. • j -il .1 ,, , : ; {. ; J i • ' / - _ J ■ ; • * * * a .5 JF%! 1He fame things being ptjc as in the precedent, r88. A I fay, that if on the circumference of the cir¬ cle B B as a bafe, we defcribe die Epicycloid B H, whofe gene¬ ral ing circle is D E R,and Radius the line AD, the crooked line of this Epicycloid being join'd to the Radius C D of the bale, and not making with it the fame mixt line, as vi the pofitioh where it was defcribed, in any place which C B is placed out of C A ; and the end D of the line A D, being put on the E- ptcycloid in E, the power Z which is applied in E, at the end of A E, as Vis in the precedent proportion, will be in Equi- fibrio with the fame power Z, which is applied in B to the end B of the line C B, and which adts on the point E by means of thecufve of the Eyicycloid B E? * Fig: n88. *Tis eafy to fee in this figure by the forming of the Epicycloid, that in any poftion, which the line C B is in, which is joined to the Epicycloid, the Arches B B will be always equal in length to the arches D E of the circle D E R • wherefore let C B be in any place, and the power applied in B cannot move it felf through One arch B B; without moving the other force applied in E on the end of the leaver A E, by an arch E E equal in length to the arch B B , whence it follows, that the powers being equal they wall remain in Equilibrioj which was to be demon ft raced. Fig. 189. ‘We may alfo make this Demoriftration as in the precedent propofttion ; and we fhall find that the fame me¬ thod which is managed in the’inequality of powers, will lead us here to equality by compounded Reafon: For if we fup- pofe that the end E of the leaver A E hath the power X A, which a&$ according as E G perpendicular to A E, and that in the point *Es At the end of G E, there be a power ^Wvhicityards according as- E F perpendicular to C E; Tis evident by'‘the nature of the Epicycioid, - thsfr the line N E drawn by the end N of the diameter D A N to the point E, will touch the EpR cycloid in that point; and that as when the point E of the end of the leaver G E fhall have run over a (pace E F indefinitely final], the fame point E of the end of the leaver A E will be come to G, w here the line F G, parallel to E N, meets E G pecpendfcularto A Eg for the ffeli portion F G of the Touch- ant$

Licence and re-use

Contents

Volumes