Genetics and the epidemiology of chronic diseases : a symposium, June 17-19, 1963, Ann Arbor, Michigan ... / edited by James V. Neel, Margery Shaw, William J. Schull.

Date:
1965
Catalogue details

Licence: Attribution-NonCommercial 4.0 International (CC BY-NC 4.0)

Credit: Genetics and the epidemiology of chronic diseases : a symposium, June 17-19, 1963, Ann Arbor, Michigan ... / edited by James V. Neel, Margery Shaw, William J. Schull. Source: Wellcome Collection.

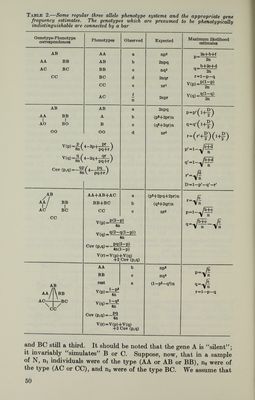
    60/412 (page 50)
    where Ipp=2N[2(l-q)^+q(r+2p)]/r(r+2p) Ipq=:2N[r+pr+2p]/r(r+2p) I,,=2N[r2(2-r) + 2pq(l + r) + q='r]/qr(4+2p). Now the variances are merely o'p=lQq/D Cpq^ Ipo/D where D=I T —P Qq pg* Though the algebraic expressions for the variances and covariances are quite cumbersome, numeric values can be readily obtained in the manner just described. Once one has generated a set of estimates, what then? Of immediate interest, of course, is the rehability of the estimates; this hinges upon the appropriateness of the genetic model, the randomness of the sample, etc. Let us examine briefly the more important of these. First, is the model appropriate? This can be tested directly from the data from which the estimates are obtained whenever the number of phenotypes exceeds the number of parameters to be estimated by at least one. Under these circumstances one merely compares the observed numbers of individuals in the various phenotypes with those expected, and the signiñcance of the discrepancies which are en¬ countered can be evaluated by chi-square. If, as in the present case, the number of phenotypes does not satisfy the stricture just cited, the appropriateness of the model cannot be tested in the manner described. However, if data exist on two generations, it is generally possible to test the model indirectly through a test based upon the frequency of segregating families (see, for example, Neel and Schull, 1954, pp. 200-203). In either event, it must be borne in mind that the model involves two major assumptions; namely, that the genotype-phenotype correspondences are as postulated and that the population sampled is in Hardy-Weinberg equilibrium. Thus, if the model is deemed inappropriate because of an improbably large chi-square, one does not necessarily conclude that the genotype-phenotype correspondences are not as postulated. The poor fit of the model to the data may result because (a) the genotype-phenotype correspondences are not as postulated but the population satisfies the equilibrium conditions, or (b) the genotype-phenotype correspondences are as postulated but the population is not in equilibrium, or (c) neither assumption holds. 52