Volume 1

Astronomie / Par M. de La Lande, Conseiller du Roi, Lecteur Royal en mathematiques; Membre de l'Academie Royale des Sciences de Paris; de la Societe Royale de Londres; de l'Academie Imperiale de Petersbourg; de l'Academie Royale des Sciences & Belles-Lettres de Prusse; de la Societe Royale de Gottingen; de l'Institut de Bologne; de l'Academie des Arts etablie en Angleterre, &c. Censeur Royal.

  • Jérôme Lalande
Date:
M.DCC.LXIV. Avec Privilege du Roi
Catalogue details

Licence: Public Domain Mark

Credit: Astronomie / Par M. de La Lande, Conseiller du Roi, Lecteur Royal en mathematiques; Membre de l'Academie Royale des Sciences de Paris; de la Societe Royale de Londres; de l'Academie Imperiale de Petersbourg; de l'Academie Royale des Sciences & Belles-Lettres de Prusse; de la Societe Royale de Gottingen; de l'Institut de Bologne; de l'Academie des Arts etablie en Angleterre, &c. Censeur Royal. Source: Wellcome Collection.

    838/878 (page 10)
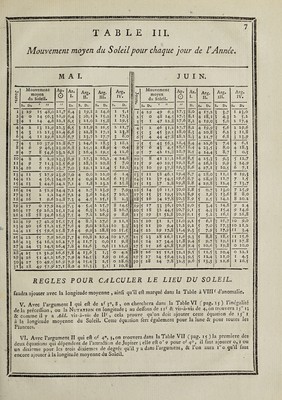
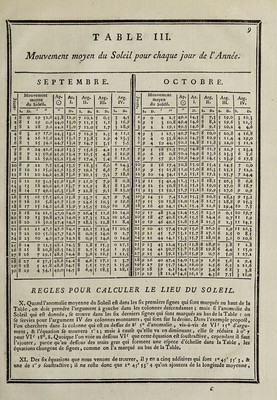
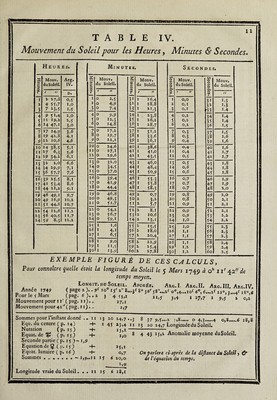
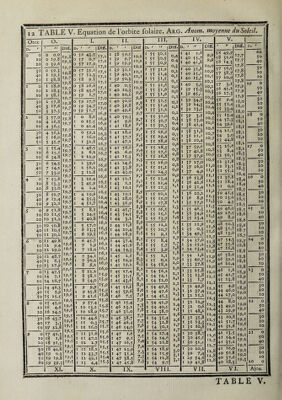
    Mouvement moyen du Soleil pour chaque jour de VAnnée, i K 3 4 5 6 7 8 9 10 11 12 ïï H M I6j *7! 18 19 zo 21 22 23 24 2* 26 27 ! 28 29 30 N 0 V ] E M B R E. D É C E M B R E. Mouvement moyen du Soleil. Ap. Q Ar. 1. Arg. 11. Arg. 111. Arg. IV. <-« O Mouvement moyen du Soleil. Ap. O Ar. 1. Arg. II. Arg. 111. Arg. IV. s. D. / n // D. S. D. s. V>. s. D. • S. D. « H tl D. s. D. s. D. s. D. 10 O 37 20,7 s 4,7 16,2 9 * ,2 6 8,0 3 28,2 1 11 O 11 3 0,6 60,1 17,8 10 2,3 6 26,5 4 3>9 to I 36 29,0 54,9 16,2 9 6,1 6 8,6 4 10,4 2 II I 10 38,9 60,3 .17,8 10 3.2 6 27,1 4 l6,l 10 2 3? 37>4 11,1 16,3 9 7,o 6 9,3 4 22,6 3 II 2 9 47,3 60,5 • 17,9 10 4,1 6 27,8 4 28,3 10 3 34 4*,7 *5,3 16,3 9 7,9 6 9,9 * 4,8 4 11 3 8 5*,6 60,7 17,9 10 *,0 6 28,4 * 10,* 10 4 33 *4,0 16,4 9 8,8 6 «o,î * 16,9 * 11 4 8 3>9 60,8 l8,0 10 * 9 6 29,0 5 22,7 10 5 33 2,4 *1,6 «6,4 9 9,7 6 11,1 * 29,1 6 11 5 7 12,3 61,0 18,0 10 6,8 6 29,6 6 4,9 10 6 32 10,7 *5,8 16,5 9 10,6 6 11,7 6 11,3 7 il 6 6 20,6 61,2 18,1 10 7,7 7 0,2 6 17,0 10 7 31 19,0 56,0 • 6,* 9 ii,6 6 12,3 6 23,5 8 11 7 * 28,9 61,4 18,1, 10 8,6 7 0,8 6 29,2 10 8 3° 27,3 56,2 16,6 9 I2>* 6 13,0 7 *,7 9 11 8 4 37,3 61,6 18,2 ylO 9,5 7 1,* 7 1 I >4- 10 9 2 9 3*,7 *6,4 16,6 9 «3’4 6 13,6 7 17,9 10 II 9 3 45,6 61,7 18,2 IO 10,4 7 2,1 7 23,6 10 10 28 44>° *6,5 16,7 9 *4,3 6 14,2 8 0,1 II 11 10 z 53.9 61,9 18,3 IO II.3 7 2,7 8 *,8 10 il 27 52,3 *6,7 16,7 9 î*,2 6 14,8 8 12,3 12 II 11 2 2»3 62,7 18,3 IO 12,2 7 3>3 8 18,0 10 12 27 o,7 *6,9 16,8 9 16,1 6 1 *,4 8 24,* *3 il 12 1 10,6 62,3 18,4 IO 13,1 7 3 >9 9 0,2 10 13 26 9,0 *7,1 16,8 9 17,0 6 16,0 9 6,7 «4 II «3 0 18,9 62,y 18,4 IO 14,0 7 4,5 9 12,4 10 14 2? 17,3 *7,3 16,9 9 17,9 6 16,6 9 18,8: 1* 11 13 *9 27,2 62,6 18,5 IO 14,9 7 * ,2 9 24,6 10 15 24 25,7 57,4 16,9 9 18,8 6 «7,3 10 1,0 16 11 14 *8 3 î>6 62,8 18,5 IO i*,8 7 5,8 10 6,8 10 16 23 34,o *7,6 17,0 9 19,7 6 17,9 10 13,2 17 II 1* *7 43,9 63,0 18,6 IO 16,7 7 6,4 10 19,0 10 17 22 42,3 *7,8 17,0 9 20,6 6 «8,* 10 2*,4| 18 11 16 *6 *2,2 63,2 18,6 IO 17,6 7 7,0 11 M 10 18 21 5:0,6 *8,0 »7,i 9 21,* 6 19,1 11 7,6 19 11 17 *6 0,6 63,4 18,7 IO 18,6 7 7,6 11 «3>3 10 19 20 ■59,0 *8,2 17,2 9 22,4 6 «9,7 11 19,8 20 11 18 5* 8,9 63,* 18,7 10 19,5 7 8,2 11 2*,* 10 20 20 7,3 *8,3 «7,2 9 23,3 6 20,4 0 2,0 21 II 19 *4 17,2 63,7 18,8 IO 20,4 7 89 0 7,7 10 21 19 i*,6 *8,* «7,3 9 24,2 6 21,0 0 14,2 22 II 20 *3 2*,5 63.9 18,9 IO 21,3 7 9,5 0 19,9 10 22 18 24,0 *8,7 17,3 9 25,1 6 21,6 a 26,4 23 11 21 *2 33.9 64,1 18,9 10 22,2 7 10,1 I 2,1 10 23 17 32’3 *8,9 «7,4 9 26,0 6 22,2 1 8,6 24 11 22 *1 42,2 64,3 19,0 10 23,1 7 10,7 I 14,3 10 24 16 4°,6 *9,o 17,4 9 26,9 6 22,8 1 20,8 2* 11 23 *0 *0,* 64,4 19,0 10 24,0 7 ir,3 I 26,5 10 25 15 49,0 59,2 «7,5 9 27,8 6 23,4 2 2,9! 26 11 24 49 *8,9 64,6 19,1 10 24,9 7 n,9 2 8,7 10 26 14 57,3 *9,4 «7,5 9 28,7 6 24,1 2 I^Ij 27 ] 1 2* 49 7,2 64,8 19,1 10 2?,8 7 12,6 2 20,9 10 27 14 5,6 *9.6 17,6 9 29,6 6 24,7 2 27,3 28 11 26 48 «5,5 65,0 19,2 10 26,7 7 H,2 3 3.1 10 28 «3 14,0 *9,8 17,6 10 0,* 6 25,3 3 9,* 29 11 27 47 23,8 65,2 19,2 10 27,6 7 13,8 3 1*,2 10 2 9 12 22,3 *9.9 «7,7 IO 1,4 6 2*,9 3 21,7 3° 11 28 46 32,2 6*,3 19,3 10 28,*. 7 i4,4 3 27,4 ! 31 U 29 4* 4°,* 6*,* 19,3 10 29,417 i*,o 4 9,6 REGLES POUR CALCULER LE LIEU DU SOLEIL. nf 13® io' 24 7 , ou bien on ajoutera d’abord toutes les équations additives pour fouftraire enfuite celle qui eft négative , & l’on aura la longitude vraie du Soleil nf 150 6' 18 1 pour le temps moyen propofé. XII. Suppofons que le temps propofépour lequel on a entrepris le calcul du lieu du Soleil, foit un temps vrai ,c’eft-à-dire , qu’on demande le lieu du Soleil pour le 5 Mars oh 11' 42 'de temps vrai : on luppofera d’abord que c’eft un temps moyen , & l’on fera tous les calculs précédents ; mais on trouvera en luivant l’explication des Tables XIII & XIV, qu il faut ajouter 11' 47 4 au temps vrai, pour avoir le temps moyen correfpondantdont on aurait dû Ce fervir; ajoutant donc cette équation , l’on aura le temps moyen oh 23' 29' 4; l’on recommencera le calcul du lieu du Soleil peur ce temps moyen, ou ce qui revient au même , on ajoutera au lieu du Soleil déjà trouvé le mouvement du Soleil pour 11' 47 ' qui eft de 29, & l’on aura le lieu du Soleil pour oh 11 ' 42 de temps vrai, qui eft la même chofe oh 13' 29' de temps moyen. 4 que