Volume 1
Astronomie / Par M. de La Lande, Conseiller du Roi, Lecteur Royal en mathematiques; Membre de l'Academie Royale des Sciences de Paris; de la Societe Royale de Londres; de l'Academie Imperiale de Petersbourg; de l'Academie Royale des Sciences & Belles-Lettres de Prusse; de la Societe Royale de Gottingen; de l'Institut de Bologne; de l'Academie des Arts etablie en Angleterre, &c. Censeur Royal.
- Jérôme Lalande
- Date:
- M.DCC.LXIV. Avec Privilege du Roi
Licence: Public Domain Mark
Credit: Astronomie / Par M. de La Lande, Conseiller du Roi, Lecteur Royal en mathematiques; Membre de l'Academie Royale des Sciences de Paris; de la Societe Royale de Londres; de l'Academie Imperiale de Petersbourg; de l'Academie Royale des Sciences & Belles-Lettres de Prusse; de la Societe Royale de Gottingen; de l'Institut de Bologne; de l'Academie des Arts etablie en Angleterre, &c. Censeur Royal. Source: Wellcome Collection.
857/878 (page 29)
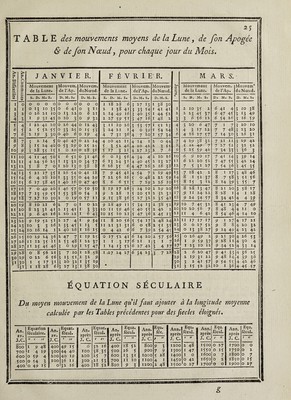
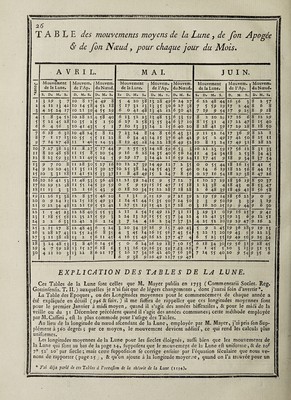
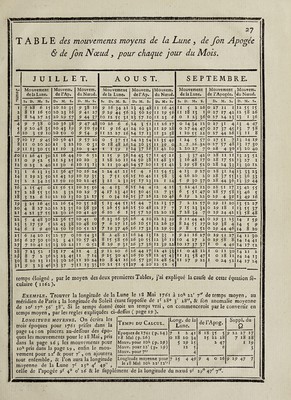
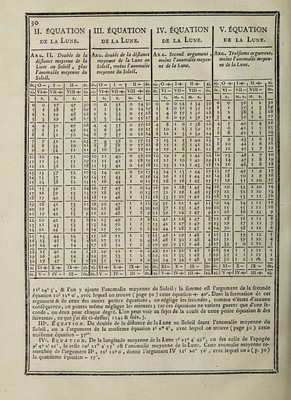
![TABLE du moyen mouvement de la Lune, de f on Apogée & de fon Nœud, pour les heures, minutes & fécondés. 29 : n> e Lune • Apo. 0 ! 09 • Ü M. s. M • S* I 0 32 J6 O 17 2 I 5 *3 O 33 I ^ 1 ?8 4 9 O 5° 1 4 2 11 46 I 7 I 5 2 44 42 I 24 1 6 3 17 39 I 40 1 7 3 50 35 I 57 4 23 31 2 14 I 9 4 56 28 2 3° i i° J i 9 25 2 47 ijn 6 z 21 3 4 li z 6 3 J 18 3 21 13 7 8 14 3 37 -M 7 4i 10 3 54 M 8 H 7 4 11 16 8 47 3 4 27 17 9 20 0 4 44 18 9 52 0 J 1 18 10 ZJ 53 f 18 19 10 î8 4 9 J 34 21 II 3* 46 J 51 22 12 4 42 6 8 *3 12 37 39 6 24 | 14 •3 10 35 6 4i Nœud Lune. Ap. N. s. a Lune. M. M. s. s. M. s. M. S. S. s. T. T. T. S. s. T. O 8 ] 0 33 O O 31 17 I O 16 2 1 6 I O 32 17 34 O 24 3 1 39 I O 33 18 7 0 32 4 2 12 I I 34 18 40 O 40 5 2 45 I I 35 19 13 O OO 6 3 18 2 I 36 19 46 O 56 7 3 51 2 T 37 20 19 I 4 8 4 24 3 1 38 20 52 I 12 9 4 56 3 1 39 21 25 I 1? ro 5 29 3 T 40 2^ 58 I 2-7 11 6 2 3 1 4' zz 3 1 I 35 12 6 35 3 2 42 23 4 I 43 *3 7 8 4 2 43 23 36 I 51 14 7 41 4 2 44 24 9 I 59 15 8 14 4 2 45 24 42 2, 7 16 8 47 4 2 46 25 15 2 M 17 9 20 5 2 47 2 5 48 2 23 18 9 53 5 M 48 26 21 2 31 19 10 2 6 5 3 49 26 54 2 39 20 xo 59 6 3 50 ^7 27 £ 4.7 21 11 32 6 3 51 28 0 2 55 22 12 5 6 3 52 28 33 3 3 Z3 12 38 6 3 53 29 6 3 il 24 T3 r 1 7 3 54 29 39 25 13 44 7 3 55 30 12 26 H 16 7 3 56 3° 45 27 14 49 8 4 57 3i 18 28 15 22 8 4 58 3i 51 29 15 55 8 4 59 32 24 /30 16 28 8 4 60 32 56 A. N. S. T. 9 9 9 9 10 to 10 11 11 11 t r T 2 12 12 r31 6 J3 *3 13 14 H 14 14 i? 11 1J 16 16 16 16 17 ) I. ÉQUATION ANNUELLE. Arg Anomalie moyenne du Soleil. ï Aj. Aj. Ajout. Ajout. Aj. Aj. | O. I. II. III. IV. V. M . S* M . s. M. S. M. s. M . s. M . s. 0 O O 5 31 9 40 II 20 9 58 5 49 3Ô 1 O 12 5 41 9 46 I I 20 9 5 2 5 39 29 i 2 O 24 5 5i 9 52 11 20 9 46 5 28 28 3 O 35 6 1 9 58 I I 20 9 39 5 17 27 4 O 47 6 11 10 3 11 19 9 33 5 6 26 5 O 58 6 21 10 9 I I 19 9 26 4 55 25 1 6 I 10 6 3° 10 14 11 18 9 19 4 44 24 ! ~ I 21 6 40 10 19 I I 17 9 12 4 33 23 i 8 I 33 6 49 10 24 II 16 9 5 4 22 22 I 9 I 44 6 58 10 29 I I 15 8 58 4 i I 21 110 I 55 7 7 10 33 11 13 8 5i 3 59 20 11 r 2 7 7 16 10 37 II 11 8 43 3 48 19 1r2 £ 18 7 25 10 41 11 9 8 35 3 36 18 Tj 2, 2.Q 7 34 10 45 I I 7 8 27 3 25 IZ 14 i 40 7 42 10 49 I I 5 8 19 3 13 16 15 £ 5i 7 5 f 10 52 I I 2 8 11 3 I f 5 116 3 2 7 59 10 55 IO 59 8 3 2 5° 14 1 3 23 8 7 10 58 IO 56 7 54 2 38 13 | 18 3 24 8 15 II 1 IO 5 2 7 45 £ 2 6 12 1 ^ 3 35 8 z3 11 3 IO 49 7 36 2 M TT i10 3 46 8 3i 11 6 IO 45 7 27 2 £ 10 Zl 3 57 8 39 11 8 10 41 7 18 I 50 9 !22 4 8 8 46 11 10 10 37 7 9 I 38 8 23 4 18 y 54 11 12 IO 33 7 O I 26 7 24 4 29 9 1 11 H 10 29 6 30. I M 6 25 4 40 9 8 11 16 10 24 6 40 I 1 3 26 4 5° 9 15 11 17 10 19 6 3° 0 49 4 27 5 O 9 21 11 18 10 14 6 zo O 37 3 28 5 11 9 28 11 19 10 9 6 9 O 25 2 29 5 2 1 9 34 11 20 10 4 5 59, O 13 1 i30 5 31 9 40 11 20 9 58 5 491 O 0 0 i ! II. 10. IX. VIII. VII. VI. ôtez. ôtez. ôtez. ôtez. ôtez.1 ôtez. Éq_uat 10 N séculaire. Si l’on vouloit calculer le lieu de la Lune pour un fiecle fort éloigné, par exemple, pour l’an 250 de J. C. on ajouteroit l’époque de l’année zoo (page 23 ) avec le mouve¬ ment pour jo ans (page 24) & le mouvement du jour propofé; après avoir ainfî trouvé la longitude moyenne, comme dans l’exemple précédent, on y ajouteroit l’équation féculaire (page 23 ) qui , pour l’année zjo , Ce trouve de 23' 30 par un milieu entre zi' J3 & 23' 7. J’ai expliqué ailleurs les caufes de cette équation féculaire ( 1 idi), j’ajouterai feulement ici que la néceflité de cette équation féculaire paroit être prouvée, non feulement par deux obfervations arabes dont nous avons parlé, mais encore par¬ les obfervations faites depuis 60 ans: M. Mayer a trouvé le mouvement moyen pour 60 ans de if 10® 43' 24 plus grand d’une ou deux minutes, que ne le donnent les anciennes obfervations , toutes les éclipfes du dernier Gecle s’accordent à la minute avec cette accélération, tandis que les erreurs vont à 2 ou 3 minutes, quand on employé le mouvement moyen des autres Tables; enfin 42 obfervations de M. de la Hire, calculées enfuite par M. Bailly avec le plus grand foin , paroiffent indiquer qu’il fau- droit encore ajouter environ 38” au mouvement pour 60 ans établi par M, Mayer. Équation annuelle. Avec l’anomalie moyenne du Soleil ior 170 57', on trouvera (pag. 29) l’équation annuelle — 7’ 25 '; j’ai donné ci-devant l’hiftoire de cette équation annuelle ( 1136 )°& fa caufe (2795). IIe. E q_uat 10 N. De la longitude moyenne de la Lune, on retranche celle du Soleil if 2S0 3' 28, a 5f 270 i' 11 j diftance moyenne de la Lune au Soleil ; on double cette diftance , ce qui donne on a h](https://iiif.wellcomecollection.org/image/b30412821_0001_0857.jp2/full/800%2C/0/default.jpg)