Volume 1

Astronomie / Par M. de La Lande, Conseiller du Roi, Lecteur Royal en mathematiques; Membre de l'Academie Royale des Sciences de Paris; de la Societe Royale de Londres; de l'Academie Imperiale de Petersbourg; de l'Academie Royale des Sciences & Belles-Lettres de Prusse; de la Societe Royale de Gottingen; de l'Institut de Bologne; de l'Academie des Arts etablie en Angleterre, &c. Censeur Royal.

  • Jérôme Lalande
Date:
M.DCC.LXIV. Avec Privilege du Roi
Catalogue details

Licence: Public Domain Mark

Credit: Astronomie / Par M. de La Lande, Conseiller du Roi, Lecteur Royal en mathematiques; Membre de l'Academie Royale des Sciences de Paris; de la Societe Royale de Londres; de l'Academie Imperiale de Petersbourg; de l'Academie Royale des Sciences & Belles-Lettres de Prusse; de la Societe Royale de Gottingen; de l'Institut de Bologne; de l'Academie des Arts etablie en Angleterre, &c. Censeur Royal. Source: Wellcome Collection.

    861/878 (page 33)
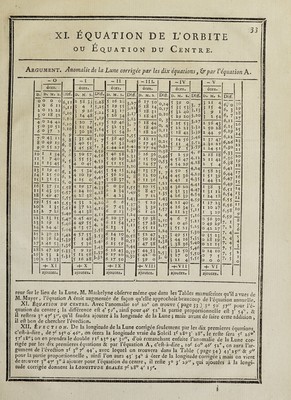
    ou Équation du Centre. 33 Argument. Anomalie de la Lune corrigée par les dix équations, & par V équation A. -IV ôtez. D. M» S* 5 39 0 5 35 53 5 3Z 40 5 29 20 5 25 53 5 22 21 5 18 42 5 14 56 5 11 4 5 7 5 5 2 59 4 58 47 4 54 29 4 5° 5 4 45 36 4 41 1 4 36 20 4 31 33 4 26 39 4 21 40 4 16 34 4 II 23 467 4 0 46 3 55 21 3 49 51 3 44 16 3 38 36 3 32 50 3 27 0 3 21 4 -t-VI I ajoutez. - V ôtez. V. M. S. 3 21 4 3 *5 4 3 9 1 3 2 *4 2 56 43 2 50 28 2 44 9 2 37 47 23121 2 24 2 18 18 2 II 42 2 f 4 I 58 23 1513? 1 44 52 1 38 3 1 31 12 1 24 18 1 17 23 1 10 27 1 3 29 0 56 30 0 49 29 0 42 27 0 35 23 0 28 19 0 21 15 0 14 10 075 000 ■4- VI ajoutez. - o ocez. D.1 n. m. s. o o o o I O 6 ii Z O 12 z2 5° I8 32 4 o Z4 4Z JiO 30 52 6 o 37 z 7 ° 43 1 1 g o 49 I9 9,° U 27 10 I i 34 11 I 7 40 *2,r *3 45 *3 I 19 48 14 I 2 f 40 15 I 31 52 16 1 37 52 11 I 43 50 18 1 49 47 19 1 55 42 20 2 1 35 21 2 726 22 2 13 15 23 2 19 2 24 2 24 46 25 2 30 32 2 6 2 3 6 14 27 2 41 53 28 2 4 7 29 29 2 53 2 \o 2 58 33 4- XI ajoutez. L>iff. 6,il 6,U 4.10 6.10 4.10 6.10 6» 9 6, 8 6, 8 4, 7 4, 4 5, 5 3 4, 2 6, z 4, o 5,53 5’57 5,55 5*53 5,5i 5,49 5,47 5,44 5,44 î,4i 5,39 5,36 - I ôtez. D . M S. 2 58 33 3 4 1 3 9 26 3 H 48 3 20 7 3 25 24 3 30 3» 3 35 48 3 40 55 3 45 58 3 50 57 3 55 53 4 0 45 4 5 34 4 10 19 4 15 0 4 19 37 4 24 10 4 28 33 4 33 2 4 37 22 4 41 38 4 45 49 4 49 55 4 5 3 57 4 57 55 5 I 48 5 5 36 5 9 19 5 12 56 5 16 28 4- X ajoutez. Diff. 5.28 5,25 5,ü 5.19 5U7 5**4 5.10 5, 7 5, 3 4,59 4,56 4.52 4,49 4,45 4,41 4.37 4,33 4.28 4,24 4.20 4,16 4.11 4, 4 4, 2 3,58 3.53 3,48 3,43 3.37 3>3Z - II ocez. u . M. s. 5 16 28 5 *9 55 5 23 17 5 26 34 5 29 46 5 3Z 53 5 35 54 5 33 49 5 4i 38 5 44 21 5 46 58 5 49 29 5 5f 55 5 54 15 5 56 29 5 58 37 6 0 39 6 2 34 6 4 23 5 6 6 6 7 43 6 9 13 6 10 57 6 Il 54 6 *3 5 4 14 10 6 *5 « 6 *5 59 6 16 43 6 17 20 6 17 5o -h IX ajoutez. - III. Diff, 3,27 3,22 3U7 3,*2 h 7 3, 1 2,55 2,49 2,4 > 2,37 2,31 2,26 2,20 2,14 2, 8 2, 2 1 >5 5 t,49 *>43 M7 1,30 1,24 M7 1,11 l, 5 0,58 o>5i °>44 o,37 0,30 ôtez. D. M. s. 6 17 50 6 18 14 61831 5 18 41 6 18 44 4 18 40 61820 6 18 11 6 17 46 6 17 14 6 16 36 6 15 50 6 14 57 6 13 57 6 12 50 6 11 3 6 6 10 15 6 8 47 6 712 6 5 29 6 3 37 6 142 5 59 38 5 57 28 5 55 11 5 52 47 5 50 16 5 47 38 5 44 53 5 42 0 5 39 0 -4- VIII ajoutez. Diff 0,24 0,17 0,10 °, 3 o, 4 0,11 0,18 0,2s 0,32 0,38 0,46 o,53 I, o 1, 7 1,14 1,21 1,28 *>35 *>43 1,50 i>57 2, 4 2, TC 2,17 2,24 M1 2,38 2,45 *»53 3, o b 7 3>r3 3,20 3,32 3.39 3.46 3,52 3.59 4, 4 4D2 4,18 4.24 4.29 4.35 4,4i 4.47 4.54 4.59 5, 6 5,n 5,16 5,21 5.25 5.30 5.35 5.40 5,46 5,5o 5.54 Diff 3° 29 28 27 26 25 24 6, o 4, 3 4, 7 6,11 4,13 4,19 4,22 6,7.6 4,30 4.33 4.34 4,38 4,4* 4,44 4,47 4,49 4,51 6.54 6.55 6,561 6,58 j10 1 9 8 7 6 23 22 21 20 19 18 *7 16 *5 M *3 12 1 r 6,59 7, I 7, 2 7» 7, 7, 7, 7, 5 7, 5 reur fur le lieu de la Lune. M. Maskelyne obferve même que dans les Tables manufcrites qu’il a vues de M. Mayer, l’équation A étoit augmentée de façon qu’elle approchoit beaucoup de l’équation annuelle. XI. Equation du centre. Avec l’anomalie iof 20° on trouve (page 33) 30 ^0' p0ur ]’£_ quation du centre; la différence ell 4’59, ainfî pour 46' 52 la partie proportionnelle ell 3' 54'S & il reliera 30 47' V> qu’il faudra ajouter à la longitude de la Lune ; mais avant de faire cette addition , il efl bon de chercher l’éveélion. XII. É section. De la longitude de la Lune corrigée feulement par les dix premières équations c’efl-à-dire , de 7f 2j° o' 46, on ôtera la longitude vraie du Soleil if 2803' 28, le relie fera 5f 26°’ 57'18; on en prendra le double rif 23° 54' 30, d’où retranchant enfuite l’anomalie de la Lune cor¬ rigée par les dix premières équations & par l’équation A, c’eft-à-dire, iof io° 4 6' 52, on aura l’ar¬ gument de l’éveélion if 30 7' 44, avec lequel on trouvera dans la Table (page34) 43'25'' & 9 pour la partie proportionnelle , ainfî l’on aura 43' 34 à ôter de la longitude corrigée ; mais on vient de trouver 3°47' 3 à ajouter pour l’équation du centre, il relie 30 3' 29, qui ajoutées à la longi¬ tude corrigée donnent la Longitude égalée 7f 28° 4' 15.