Volume 1

Astronomie / Par M. de La Lande, Conseiller du Roi, Lecteur Royal en mathematiques; Membre de l'Academie Royale des Sciences de Paris; de la Societe Royale de Londres; de l'Academie Imperiale de Petersbourg; de l'Academie Royale des Sciences & Belles-Lettres de Prusse; de la Societe Royale de Gottingen; de l'Institut de Bologne; de l'Academie des Arts etablie en Angleterre, &c. Censeur Royal.

  • Jérôme Lalande
Date:
M.DCC.LXIV. Avec Privilege du Roi
Catalogue details

Licence: Public Domain Mark

Credit: Astronomie / Par M. de La Lande, Conseiller du Roi, Lecteur Royal en mathematiques; Membre de l'Academie Royale des Sciences de Paris; de la Societe Royale de Londres; de l'Academie Imperiale de Petersbourg; de l'Academie Royale des Sciences & Belles-Lettres de Prusse; de la Societe Royale de Gottingen; de l'Institut de Bologne; de l'Academie des Arts etablie en Angleterre, &c. Censeur Royal. Source: Wellcome Collection.

    863/878 (page 35)
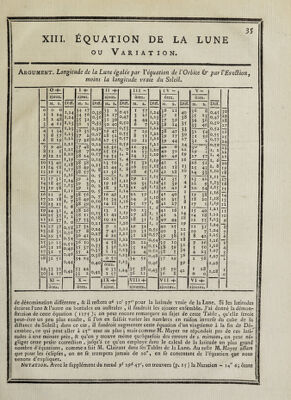
    ou Variation. 3$ Argument. Longitude de la Lune égalée par Y équation de l'Orbite & parVEveftion, moins la longitude vraie du Soleil. O -f- 1 ■h II 4- 1 j IV — V - ajout. ajout. ajout. ôtez. ôtez. ôtez. M. s. Diff. M. s. Diff. M. s. Diff. M. s. Diff. M. s. Diff. M. s. Diff. 0 I Z O 1 2 0 14 43 1,24 1,24 34 34 35 17 56 32 o,3 9 0,36 33 32 31 z 17 3° 045 0.47 I 3 4 57 21 44 1,24 1,23 36 37 37 21 I 39 40 38 36 35 34 8 23 36 0,45 o,47 30 19 28 3 4 11 1,23 36 5 3 30 40 0,50 6 7 r>23 38 14 35 33 46 o,jo 17 4 5 34 1,23 36 35 0,30 19 47 °»5 3 7 19 38 47 33 32 54 0,52 26 5 6 57 1,23 37 2 0,27 28 5i 0.55 8 51 L ,22 3 9 17 3° 31 59 o.55 15 6 8 19 I , Z h 37 26 0,14 17 55 o,57 10 12 r,n 39 44 17 31 2 o,57 24 7 9 40 I 37 48 0,1 z 26 56 11 33 1,21 40 8 24 3° 3 °,59 23 8 9 11 12 1 21 1,21 1,20 3» 38 7 24 0,19 0,17 15 14 56 54 * J w 1, 1 T. A 12 H 53 J3 1,2 O I >20 40 40 3° 49 2 2 19 16 19 17 i 57 i, 2 I» 4 22 21 10 *3 40 *>l9 T l8 38 38 Oj 14 23 5o A> T* 1, 6 15 32 M9 41 5 26 5i I» 6 20 11 H 58 38 49 ^ Q 22 44 I 8 16 5° 1,18 41 18 *3 25 43 19 12 16 15 A> 1 / I l6 38 57 0, 0 21 36 A> 0 1. 0 18 6 1,16 41 28 10 24 33 1,10 18 *3 17 3i 1,14 39 2 O T 20 27 I. T I 19 21 M5 41 35 7 23 22 I,II |I7 14 18 45 T T *7 39 3 v-'> I 19 16 20 35 1,14 4i 39 4 22 9 I,I3 16 M 19 58 I JJ 39 1 O, z 18 3 IJ A 21 48 U13 l41 41 2 20 54 I»15 15 16 ZI 9 I. O 38 56 r> *7 16 49 TTC’ 22 59 I,, I I 41 40 I ç' 19 38 1,16 14 17 22 18 y I, 7 38 49 Oj T O* U 34 A 91 J T I 24 9 1,10 T C 41 35 5 « 18 20 1,18 !3 18 23 15 i 6 38 39 O J 2 14 18 T T *7 15 17 41 17 11 17 I 1,19 12 19 14 31 I. A 38 26 *3 I 1 5 1 / 26 23 I, 6 41 16 U 40 Ij2 I I I 20 21 15 z 6 35 37 x J *T I, l 1, O 38 37 11 53 °»15 0,18 11 10 42 22 aj Ly I >20 17 28 28 31 5 3 4i |40 2 44 j4 18 *4 12 18 55 1,22 *>z3 IO 9 22 17 37 0,58 37 32 9 2 19 32 !» » 40 15 11 31 1,24 8 23 28 35 0 .c 6 37 8 0,24 7 41 3° 31 0,591 *40 3 2 2 10 7 1,24 7 24 z 9 31 0, <4 36 41 0,27 6 20 1,21 31 28 °,57 39 38 15 28 8 41 1,25 6 »5 3° 15 o,< I 36 10 °>3I 4 58 32 22 o»5 4: 39 10 7 16 1,26 ~ 26 31 16 0,49 35 37 °.33 3 36 1,2 2 33 14 0,52] 38 39 31 5 50 1,26 4 17 32 5 0,4.6 35 2 0,3 5 2 *3 1,23 34 4 0,50*33 5 34 4 23 1,*7 3 28 32 5i 34 24 0,30 0 5o t| 34 52 0,40 37 19 3b 2 56 ij 2 0,44 0,40! ôtez. T’23i 0,46 39 1,28 19 3° 33 34 35 17 0,42 33 33 44 2 0,42] 0 1 33 57 1,14 t H 36 38 21 0,43 3* 36 4i J I 0 28 0 1,28 r 0 XI - X — s IX H- VIII 4- VII 4- j VI ■4- ôtez. ôtez. P ajout. r ajoutez. ajoutez. f ajoutez. de dénomination différente, & il refiera od io’ 37 pour la latitude vraie de la Lune. Si les latitudes étoiem l'une & l’autre ou boréales ou auftrales , il faudroit les ajouter enfemble. J’ai donné ladémon- ftration de cette équation ( 117? ); on peut encore remarquer au fujet de cette Table , qu’elle feroit peut-être un peu plus exaâe, lî l’on en faifoit varier les nombres en raifon inverfe du cube de la diftance du Soleil; dans ce cas, il faudroit augmenter cette équation d’un vingtième à la fin de Dé¬ cembre, ce qui peut aller à 25 tout au plus; mais comme M. Mayer ne répondoit pas de ces lati- tudes à une minute près, & qu’on y trouve même quelquefois des erreurs de z minutes, on peut né¬ gliger cette petite corredion , jufqu’à ce qu’on employé dans le calcul de la latitude un plus grand nombre d’équations, comme a fait M. Clairaut dans fesTables de la Lune. Au refte M. Mayer aJTure que pour les éclipfes, on ne fe trompera jamais de 20”, en Ce contentant de l’équation que nous venons d’expliquer.