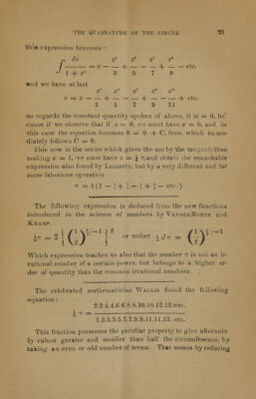The philosopher's stone / by P.H. Vander Weyde.

  • Peter Henri Van Der Weyde
Date:
1861 [i.e. 1862]
Catalogue details

Licence: Public Domain Mark

Credit: The philosopher's stone / by P.H. Vander Weyde. Source: Wellcome Collection.

Provider: This material has been provided by the National Library of Medicine (U.S.), through the Medical Heritage Library. The original may be consulted at the National Library of Medicine (U.S.)

    21/42
    THE QVaMIaTI'RE of THE CIRCLE. 1 ^ We will now give the manner of operating to find the number tt by means of the differential and integral calculus, applied to Gt.niometry ; it may serve as an illustration how the preceeding and following remarkable series are found. Let z be the arc of a circle, and Co the tangent of this are, or x = tang z for the radius = 1 All that we have to do is to find the value of s iu this equa. tion> because the whole problem is solved as soon as we know the value of an ore by its tangent, and if we could find a genera1 expression for a in a function of £, the tangent of 45° being equal to the radius, and making x = 1 we shall have \ n a and we will have the value of -. To obtain this result let us observe that the differential of the arc is — the differential of its tangent dx = dz or dz -' d tang* (o) but { sin z \ cos? . '/sin z — sin: . rfoos s i COS z I cos- 2 the differential calculus teaches us that (] sin Z = cos z.dz and d cos z c=—sin £.</;?. and substituting these values, we obtain cos'J ~ dz -f- ^nJ * ^ cos- ^ This last equation gives us, because cos' z -f sin2 8=:1, rfz rr_ con- z. rf tang 2 (b) In order to make the auxiliary quantity cos'2 z disappear, let Us remember that sin z = cos Z . tang' z and consequently COS2 r i cos' 2 .tail'- Z = 1