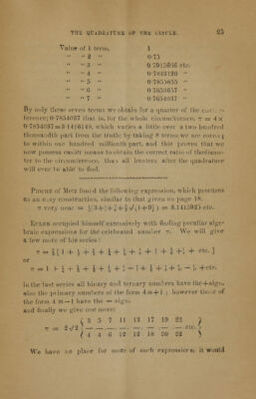The philosopher's stone / by P.H. Vander Weyde.

  • Peter Henri Van Der Weyde
Date:
1861 [i.e. 1862]
Catalogue details

Licence: Public Domain Mark

Credit: The philosopher's stone / by P.H. Vander Weyde. Source: Wellcome Collection.

Provider: This material has been provided by the National Library of Medicine (U.S.), through the Medical Heritage Library. The original may be consulted at the National Library of Medicine (U.S.)

    27/42
    T!1E QtADRATt'RB Of tHE u'IRCLH, 2il Value of I term, \ •' 2 •' 0-75 3 0 70150% etc. 4 0-7843120 ■' 5 0-7855855 6 - 0 7653657 '• 7 0-7654037 By only these seven terms We obtain for a quarter of the ci»< ferenee; 0-7854037 that is, for the whole circumference, ~r = 4X 0-7854037 = 3-1416148, which varies o little over a two hundred thousandth part from the truth; by taking' 8 terms we are correct to within one hundred millionth part, and thin proves that wc now possess easier means to obtain the correct ratio of thediame- ter to the circumference, than oil hunters after the quadrature will ever he able to find. PiocHrt of Meiz found the following expression, which procurer Os an e_isy construction, similar to that given on page 18. -r very near = K:5+'-N + § ^[1 + 9] ) ~ ^A^^'2> etc. Euleh occupied himself extensively with finding peculiar alge* braic expressions for the celebrated number -. We will give a few more of his series : Tr=|[l + ^ + l + i+^+^ + !4-^+l+ etc. ] or t = 1 h J + 1 + i + 4 + S - » + I +.i +'U - ii +etc. in the last series all binary and ternary numbers have the+sigu, also the primary numbers of the form 4tf*-j- 1 ; however th the form 4 m—1 have the — sign, and finally we give one move; C 3 5 7 11 13 17 ID 23 ) (446 12 12 18 20 22 ) Wo have r.O place for more of such expression it would