Volume 1
A mathematical and philosophical dictionary: containing an explanation of the terms, and an account of the several subjects, comprized under the heads mathematics, astronomy, and philosophy both natural and experimental: with an historical account of the rise, progress, and present state of these sciences: also memoirs of the lives and writings of the most eminent authors. Both ancient and modern, who by their discoveries or improvements have contributed to the advancement of them ... With many cuts and copper-plates / By Charles Hutton.
- Charles Hutton
- Date:
- 1795-1796
Licence: Public Domain Mark
Credit: A mathematical and philosophical dictionary: containing an explanation of the terms, and an account of the several subjects, comprized under the heads mathematics, astronomy, and philosophy both natural and experimental: with an historical account of the rise, progress, and present state of these sciences: also memoirs of the lives and writings of the most eminent authors. Both ancient and modern, who by their discoveries or improvements have contributed to the advancement of them ... With many cuts and copper-plates / By Charles Hutton. Source: Wellcome Collection.
667/696 (page 639)
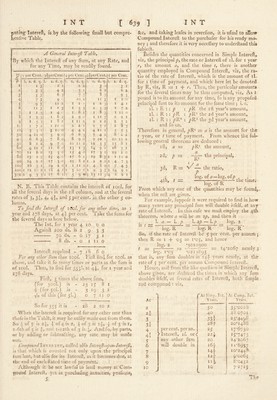
![/ piiting Intereft, is by the following fmall but compre- henlive Table. A General Interejl Tables By which the Intereft of any Sum, at any Rate, and for any Time, may be readily found. 0 3 Cent. 3lperCent. + per Cent. 4l per Cest. It per Cent. •-< cn 1. s. d. 9- 1. s. d. q- 1. c w • d. q- 1. s. d. q* 1. s. d. q. I I 3 2r I 2 2 3 0 3 I 2 3 3 4 2 5 1 6 0 6 2 3 5 3 6 3 7 8 3 9 3 4 7 3 9 C fO 2 II 3 I I 0 5 9 3 11 2 I I T I 2 3 I 4 I 6 11 3 I T 3 I 3 3 I 5 3 T 7 2 7 I I I 4 c I 6 1 I 8 3 I II 0 8 I 3 3 I 6 1 I 9 0 I 11 3 2 2 I 9 I 3 I 8 2 I 11 2 2 2 2 2 5 2 IC I 7 2 I j I c 2, 2 1 2 5 2 8 3 20 3 3 I 3 10 0 4 4 2 4 11 I 5 5 3 30 4 11 0 5 9 c 6 6 3 7 4 2 8 2 2 40 6 6 3 7 8 0 8 9 0 9 10 I 10 11 2 50 8 z 9 7 c 10 11 12 3 3 13 8 I 60 9 10 I I r 6 c 13 I 3 9 2 16 5 I *70 11 6 0 ^3 5 c 15 4 0 17 3 I 19 2 0 So 13 I 3 4 c 17 6 I 8 3 r I I I Q 90 14 9 2 17 3 c 19 8 2 I 2 2 I I 4 7 3 100 16 5 1 19 2 c I I 11 0 I 4 8 0 I 7 4 3 200 r 12 10 2 I 18 4 I 1 3 10 0 2 9 3 3 2 14 9 2 300 2 9 3 3 2 17 6 1 5 9 0 3 13 II 3 4 2 2 I N. B. This Table contains the intereft of lool. for all the feveral days in the ift column, and at the feveral rates of 3, 34, 4, 4I, and 5 percent, in the other 5 co- lumns. To Jlnd the Interejl of i(3c/. for any other time, as i year and 278 days, at 4I per cent. Take the fumsfor the feveral days as here below. The Int. for i year 410 00 Againft 200 ds. is 2 9 33 — 70 ds. - o 17 31 8 ds. - o I 11 o Intereft required - 7 18 60 For any other Sum than 100/. Firft find for lOol. as above, and take it fo many time-s or parts as the fum Is of lOol. Thus, to find for 355I. at 4I, for i year and 278 days. Firft, 3 times the above ium, (for 300].) is - 23 15 81 F (for 5’ol.) Is - 3 19 31 of ilils (for 5I.) o 7 II o So for 355 it is - 28 2 10 2 When the intereft Is .required for any other rate than thofein the Tablfe, it may be eafily made out from them. So ^ of 5 is f oi4 is 2, 4: ^f 3 is i j, | of 3 is i, I-6th of 3 is and i-i2th of 3 is And.fo, by parts, or by adding or fubtradting, any rate may be made out. Compoundcalled alfo Interejl^npon-Interefl, is that which is counted not only upon the principal ium lent, but alfo for its Intereft, as it becomes due, at tiie end of each ftated time of payment. I • Although it be not lawful to lend money at Com- p.ound Intereft, yet in purchafing annuities, penfions, 5- &c, and taking leafes in reverfion, it is ufual to allow Compound Intereft to the purchafer for his ready mo- ney ; and therefore it is very neceflary to underftand this fulfiedl. Befides the quantities concerned in Simple Intereft, viz, the principal p, the rate or Intereft of il. for i year r, the amount a, and the time /, there is another quantity employed in Compound Intereft, viz, the ra- tio of the rate of Intereft, which is the amount of iL for I time of payment, and which here let be denoted by R, viz, R I r. Then, the particular amounts for the feveral times m.ay be thus computed, viz. As I pound is to Its amount for any time, fo is any propofed principal fum to its amount for the famie time ; i. e, il. : Fv. : : ^ : yjR the ift yearns amount, ll. : R ; : : y>R^ the 2d year’s amount, il. : R : : t^R^ ; 7;)R3 the 3d year’s amount, and fo on. Therefore in general, /'R'^ = « Is the amount for the t year, or t time of payment. From whence the foI=> lowing general theorems are deduced : ift, 2d, a P 3d, 4th, R = ^R‘ the amount, —the principal. P the ratio, log. of log. of , —^ ---2 C the time; log. 01 K From which any one of the quantities may be foimdj when the reft are given. For example, fuppofe it were required to find in,how- many years any principal fum will double itfelf, at any rate of Intereft. In this cafe we muft employ the 4 th theorem, where a will be — zp, and then It \. a — \. p 1. .2/ — !•/'_ If^g* 2 ^ ^ log. R log. R log. R * So, if the rate of Intereft be 5 per cent, per annum ; then R = I + '05 log. 2 t = 1*05, and hence •3010300 , = I4’2o67 nearly 5 log. 1*05 *0211893 that is, any fum doubles in 14-f years nearly, at tho rate of 5 per cent, pci annum Conipound Intereft. Hence, and from the like queftion in Simple Intereft, above given, are deduced the times In wdiicli any fum doubles itfelf, at feveral rates of Intereft, both fimplc and compound : viz. 1 'At Simp. Tnt, At Comp. Tnt At' Years. Years. 2 50 35-0028 40 280701 3 331 23-44lyy 3^ 2Sf 20*1488 4 per cent, per an. 25 17-6750 aI k Intereft, i/. or<^ 22| 15*7473 5 any other fum 20 14-2067 6 will' double in i6t 11-8957 7 Ht 10*244^ 8 i2r 9*0065 9 ' 8*0432 0 L 7*2725 • Thff](https://iiif.wellcomecollection.org/image/b28771485_0001_0667.jp2/full/800%2C/0/default.jpg)