Volume 1
A mathematical and philosophical dictionary: containing an explanation of the terms, and an account of the several subjects, comprized under the heads mathematics, astronomy, and philosophy both natural and experimental: with an historical account of the rise, progress, and present state of these sciences: also memoirs of the lives and writings of the most eminent authors. Both ancient and modern, who by their discoveries or improvements have contributed to the advancement of them ... With many cuts and copper-plates / By Charles Hutton.
- Charles Hutton
- Date:
- 1795-1796
Licence: Public Domain Mark
Credit: A mathematical and philosophical dictionary: containing an explanation of the terms, and an account of the several subjects, comprized under the heads mathematics, astronomy, and philosophy both natural and experimental: with an historical account of the rise, progress, and present state of these sciences: also memoirs of the lives and writings of the most eminent authors. Both ancient and modern, who by their discoveries or improvements have contributed to the advancement of them ... With many cuts and copper-plates / By Charles Hutton. Source: Wellcome Collection.
669/696 (page 641)
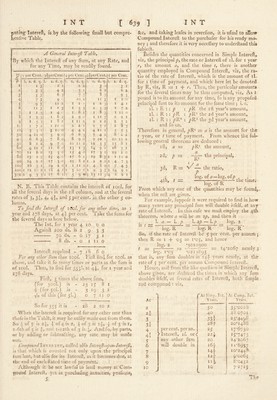
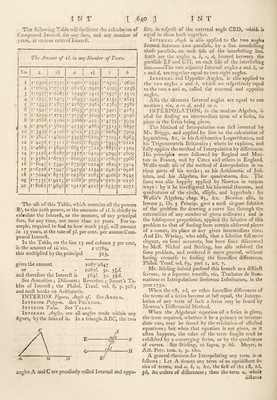
![diftance from A Is exprefled by x, will be this, viz, ‘Theorem i, Ir A*— I3C — 2. x = A -f -f* A . b X . . occ. 2 23 Now the logs, of the given numbers will be thus: 2*0043214 = a 2*0086002 = b 2*0170333 = d 2*0211893 =: e Hence, if any of the orders of differences become equal to one another, or —. o, this feries for the inter- polated term will break off, and terminate, otherwife it will run out in an infinite feries. Ex. To find the 20th tenn of the feries of cubes I,' 8, 27, 64, 125, &c, or 2h 33, 43,^53, &c. Set down the feries in a column, and take their conti- nual differences as here an- nexed, where the 4th differ- ences, and all after it be- come o, alfo A =: I, a — h — \2y r = 6, and X — 19 ; therefore the 20th term fought is barely A a I h 7 ^ 8 12 ^ 19 o 27 „ ‘8 37 6 64 125 01 24 d o 18 18 17 z = i 4.19 x'7 + 19 X— X 12+19.—.— .6 2 23 = 1 + 133+ 2052 + 5814 = 8000. Theor. 2. In any feries of eqiiidiflant terms, <7, s<i d, See, whofe firft differences are fmall; to find any term wanting in that feries, having any number of terms given. Take the equation which ftands againfl the number of given terms, in the following Table ; and by reducing the equation, that term will be found. No. 1 2 3 4 5 6 See. Equations. a — b z=z o * a •— zb c — o a ^b -i~ 30 — d e=z o a — 4^ 4- 6r — 4<7 4- e ~ o ^ — 5^ + lor — lod -4 3e — f = o a 6b 15^ — zod + i^e — 6f g ■=: o See, n n — I a — nb -]r n . c d See = o. where it is evident that the coefficients in any equation, are the uneije of a binomial 1 + 1 raifed to the power denoted by the number of the equation. Ex. Given the logarithms of 101, 102, 104, and 105 ; to find the log. of 103. Here are 4 quantities given ; therefore we mull take the 4th equation a — ^b 6r — 4<'/-4^r=o, in which it is the middle quantity or term c that is to be found, becaufe 103 is in the middle among the num- bers 101, 102, 104, 105 ; then that equation gives the value of c as follows, viz c = 1-1— -A VoL. I. 4*0256335 — b^d 4 16*1025340 = 4.5 + fubtr. 4*0255107 — a -{• e 6)12*0770233 2*0128372 the log. of 103. Theor. 3. When the terms a, h, c, d. See, arc at unequal diflances from each other; to find any inter- mediate one of thefe terms, the reft being given. Let p, q, r, s, See, be the feveral diftances of thofe terms from each other; then let Cl -c *4-0*1) = c-b ^ I /> + 74-r’E= Bt=/—B2—Br q Ll = •C2-CI Dr-D . f+74 o 4- ^ * D i d-c ^ £ + E2=—B3-B2 C2=:-i-; , r 4- ^ ■n ‘ B3 = , Sec Sec Sec Then the term z, whofe diftance from the beginning • is X, will be » = <7 + Ba' + Ca* . x—p-\- . X — p • X — p — q + La . X —p . X — p — q . X -^p — q — r + Sec, to be continued to as many terms as there are terms in the given feries. By this feries may be found the place of a comet, or the lun, or any other objedl at a given time ; by know- ing the places of the fame for feveral other given times. Other methods of Interpolation may be found in the Philof. Tranf. number 362 ; or Stirling’s Summa- tion and Interpolation of Series. INTERSCENDENT, in Algebra, is applied to quantities, when the exponents of their powers are ra- dical quantities. Thus x'^^, x^^. Sec, are intcrfccn- dent quantities. See Eunciion. INTERSECTION, the cutting of one line, or plane, by another ; or the point or line in which two lines or two planes cut each other. The mutual in- terfeftion of two planes is a right line. The centre of a circle, or conic leftion, Sec, is in the interfeOlion of two diameters ; and the central point of a quadrangle ’ is the Interfeiftion of two diagonals. INTERSTELLAR, a word ufed by fome authors, to exprefs thofe parts of the univerfe, that are without and beyond the limits of our folar fyftem. In the Interftellar regions, it is fuppofed there are feveral other fyftems of planets moving round the fixed ftars, as the centres of their refpeftive motions. And if it > be true, as it is not improbable, tlut each fixed ftar is 4 N thus 6](https://iiif.wellcomecollection.org/image/b28771485_0001_0669.jp2/full/800%2C/0/default.jpg)