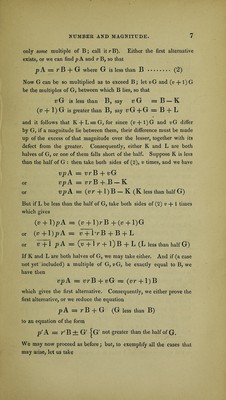The connexion of number and magnitude: an attempt to explain the fifth book of Euclid / By Augustus De Morgan.

  • Augustus De Morgan
Date:
1836
Catalogue details

Licence: Public Domain Mark

Credit: The connexion of number and magnitude: an attempt to explain the fifth book of Euclid / By Augustus De Morgan. Source: Wellcome Collection.

    16/102 (page 6)
    either 1 P is not Q’ or c X is Y/ If the first be right, the second is wrong : that is, ‘ X is not Y 7 is right.,f The preceding argument runs as follows ;—when A, B, C, &c. are all greater than Z, then 2Z, 4Z, &c. are all less than A: but 2Z, 4 Z, &c. are not all less than A ; therefore, A, B, C, &c. are not all greater than Z]. Corollary. The preceding proposition is equally true when, instead of taking more than the half at each step, we take the half itself in some or all of the steps. Prop. VI. If there be two magnitudes of the same kind, A and B, and if the scales of multiples be formed A, 2 A, 3 A, &c. B, 2 B, 3 B, &c. then one of these two things must be true; either, there are mul- tiples in the first scale which are equal to multiples in the second scale; or, there are multiples in the first scale which are as nearly equal as we please to multiples (not the same perhaps) in the second set: that is, we can find one of the first set, say m A, which shall either be equal to another in the second set, say nB, or shall exceed or fall short of it by a quantity less than a given quantity Z, which we may name as small as we please. Let us take a multiple out of each set, any we please, say pA and #B. If^A and ^B be equal, the first part of the alternative exists ; if not, one must exceed the other. Let pA exceed <?B, say by E; then we have pA = qB + E (1) Now E is either less than B, or equal to B, or greater than B. If the first, let it remain for the present; if the second, we have p A = (<7 + 1) B, or the first alternative exists : if the third, then B can be so multiplied as to exceed E. Let (t + 1) B be the first multiple of B which exceeds E; that is, let the next below, or £B, be less than E, say by G, then we have E=*B + G pA = qB + tB + G or p A =■• (q + f) B + G Now G must be less than B; for E or t B -}- G is less than (£ + 1) B, or t B -J- B. We have then made this first step (observe that q -j- t is