Copy 1

Logarithmologia or the whole doctrine of logarithms, common and logistical, in theory and practice. In three parts / [Benjamin Martin].

  • Benjamin Martin
Date:
1740
Catalogue details

Licence: Public Domain Mark

Credit: Logarithmologia or the whole doctrine of logarithms, common and logistical, in theory and practice. In three parts / [Benjamin Martin]. Source: Wellcome Collection.

    47/342 (page 25)
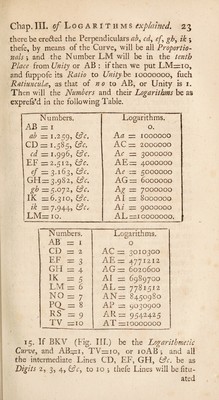
    CHAP. IV. T’he Nature of Logarithms and their Indices^ , when the Numbers are Fradtions^ farther ex-- plaind by the Logarithmic Curve. I. T Y 7E have hitherto principally confidered the Y y Nature and Properties of Logarithms of whole Numbers or Integers^ and have obferv^d that ! in the Decuple Series i, 10, 100, 1000, the I Terms have their Ratio’s to Unity affirmative ovpo- I fitive^ viz. I, 2, 3, or thus, -|-i, -|-2, +3, i ^c, the contrary of which happens when the Num- ! her of the Logarithm is not integral^ but frablional^ ; or expreffes only fome frablionate Part of Unity. For 1 there the Series being continued on the other Side^ or below Unity^ hath the Indices of the Powers of the Terms of a Sffiality diredlly oppoftte to the former; and therefore as thofe Indices were pojitive^ fo thefe I will be of a negative Nature^ and import the Terms i to be below the State of Unity^ or rather of Integrity ; ! and will be affedted with the Sign—, as—-i, —2, j —^3, ^c, as is evident Chap. III. Art. 5. ] 2. Wherefore fince AB reprefents (Fig. II.) [ all the Numbers in the Series towards the right Iland^ or above Unity^ CD, EF, GH, Cfr. being integral^ • and having the Ratio greater than Unity^ will have ! the Logarithms thereof pefitive^ viz. +AC, ~FAE, ij H-AG, &c. But thofe Numbers or Herms on the Left., or below Unity^ cd, ef, gh, S^c\ being/r^r- i tionate^ and having the Ratio lefs than Unity or de- 1 creafmg., will have the Logarithms thereof Negative, ;1 viz. —Ac, ■—Ae, -—Ag, i^c. iothflndices I E of