Tables of physical and chemical constants and some mathematical functions / by G.W.C. Kaye and T.H. Laby.

  • G. W. C. Kaye
Date:
[1941]
Catalogue details

Licence: Public Domain Mark

Credit: Tables of physical and chemical constants and some mathematical functions / by G.W.C. Kaye and T.H. Laby. Source: Wellcome Collection.

    117/200 (page 105)
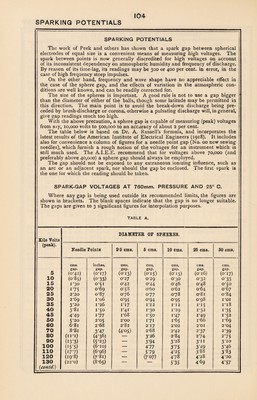
    SPARKING POTENTIALS Kilo Volts DIAMETER OF SPHERES. (peak). Needle Points. 2 5 cms. 5 ems. 10 cms. 25 cms. 50 cms. (contd.) cms. inches. cms. cms. cms. cms. cms. gap. gap. gap- gap. gap- gap. gap- 140 (24-I) (9*48) — — 5*97 5*10 4*94 150 (26-1) (io*3) —- — 6*64 5*52 5*32 160 (28-1) (II*1) —. — 7*37 5*95 5*70 170 (30*1) (n*9) —- — 816 639 6*09 180 (32*0) (12-6) —_ — 903 6*84 6*48 190 (33*9) (13*3) —«■ — 100 7*30 6*88 200 (35*7) (i4*o) — — in 776 7*28 210 (37*6) (H*8) — — (12*3) 8*24 7* 68 220 (39*5) (15*5) — — (13*7) 873 8-09 230 (4i*4) (16*3) — — (i5*3) 9*24 8*50 240 (43*3) (17*0) — — — 976 8*92 250 (45 '2) (17*8) 103 9'34 AIR-DENSITY CORRECTION TO SPARKING POTENTIALS Applicable only to sphere gaps. The following table gives the relative air density under different conditions. The figures are relative to dry air at 250 C. and 760 mm. pressure : Temp. Press. 720mm. Press. 740mm. Press. 760mm. Press. 780mm. 0° C. 1-04 1-06 1-09 1*12 10 i-oo 1-02 1-05 1-08 20 0-96 0-99 1-02 1-04 30 0-93 0-96 0-98 I-OI Within the limits of the above table, the correction factor for a sphere gap agrees substantially with the relative air density and so is small for normal conditions. Thus for a given length of spark gap, the tabulated kilovoltage in Table A must be multiplied by the appropriate correction factor. THE RONTGEN The rontgen (r) is the quantity of X or gamma radiation such that the associated corpuscular emission per 0-001293 gramme of air produces, in air, ions carrying 1 electrostatic unit of quantity of electricity of either sign (0-001293 gramme is the mass of 1 c.c. of dry atmospheric air at o° C. and 76 cm. of mercury pressure). LATTICE CONSTANTS OF CRYSTALS A crystal may be considered as a lattice generated by the continued repetition in three dimensions of a unit cell which in general contains only a small number of atoms or molecules. The crystal belongs to one or other of the seven classes—cubic, tetragonal, hexagonal, rhombohedral, orthorhombic, monoclinic or triclinic— according as one or more of the ratios between the sides is unity or not, and the angles are or are not right angles. A crystal face is denoted by a triad of integers {h, k, /), and is parallel to planes making intercepts a/h, bjk, cfl, on the three sides a, b, c of the unit cell. The distance d between successive members of the family of planes (/z, k, l) is given for the triclinic crystal by the formula _ Z(h2 . b2c2 sin2 a) -f- 2S[kl. <fo22(cos cos y — cos a)] d2 \a2b2c2{ 1 — cos2 a — cos2 ft — cos2 y + 2 cos a cos ft cos y] where a, b, c ; a, p, y are the sides and angles of the unit parallelopiped.