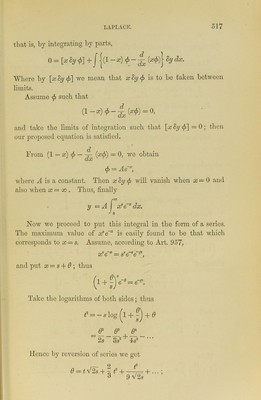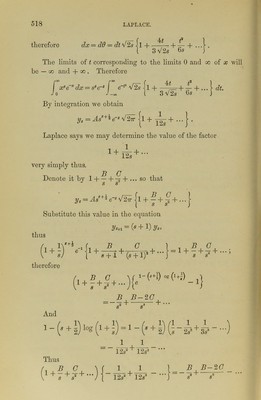A history of the mathematical theory of probability from the time of Pascal to that of Laplace / by I. Todhunter.

  • Isaac Todhunter
Date:
1865
Catalogue details

Licence: Public Domain Mark

Credit: A history of the mathematical theory of probability from the time of Pascal to that of Laplace / by I. Todhunter. Source: Wellcome Collection.

    537/648 (page 517)
    that is, by integrating by parts, o = [x By 4>] + j j(i -x) </> - ^ (#</>) j By Where by [x By <£] we mean that xBy § is to be taken between limits. Assume </> such that and take the limits of integration such that [#%(/>] = 0; then our proposed equation is satisfied. From (1 — x) cf> — (a;^>) = 0, wo obtain <j> = Ae~x, where A is a constant. Then x By cj) will vanish when x — 0 and also when x = oo . Thus, finally pco y = A I x8e~xdx. Now we proceed to put this integral in the form of a series. The maximum value of x8e~x is easily found to be that which corresponds to x = s. Assume, according to Art. 957, x8e~x = s”e~ae~t‘i, and put x = s + 6 ; thus Take the logarithms of both sides; thus = - 8 log ^1 + + 0 6>2 2s 3 3*+ -1-3 is3 Hence by reversion of series we get 6 = t 2S -}■ ~ J-r= + • • • 3 9 V2s