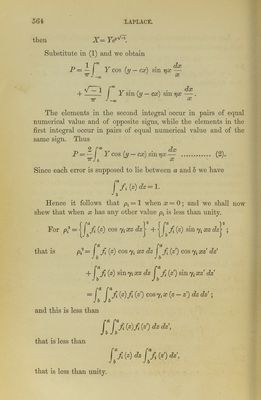A history of the mathematical theory of probability from the time of Pascal to that of Laplace / by I. Todhunter.

Isaac Todhunter

Date:: 1865

Credit: A history of the mathematical theory of probability from the time of Pascal to that of Laplace / by I. Todhunter. Source: Wellcome Collection.

586/648 (page 566)

$but no serious error will arise from this circumstance, because the true value of Y and the approximate value are both very- small when x is sensibly different from zero. We may put (3) in the form cos (lx — cx + xv) dv yx. then by changing the order of integration, and using a result given in Art. 958, we obtain 2 fv (l-c+v)2 P = JT — e I*-2 dv ] _ v This is therefore approximately the probability that E will lie between c — r) and c + rj. It is necessary to shew that the quantity which we have denoted by k is really positive; this is the case since A2 is really positive, as we shall now shew. From the definition of 7q2 in con- junction with the equation f f (z) dz = 1, we have J b 2K = Jb Pf 0) dz f [z') dz' - zfi (z) dz fbzf (z) dz Z2 - zz')f (z)fi (z) dz dz\ And so also 242 = ( [ (z2 - zz)f (z) f (z) dz dz. Jb Jb Hence, by addition, 4 K=faja (z-z'yfi(z)fi(z')dzdzf. J b J b Thus 4A2 is essentially a positive quantity which cannot be zero, for every element in the double integral is positive. It is usual to caliyj (z) the function which gives the facility of error at the 7th observation; this means that f (z) dz expresses the chance that the error will lie between z and z + dz. If the function of the facility of error be the same at every$