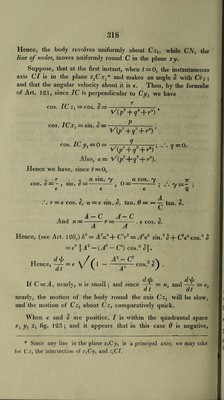A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell.

  • William Whewell
Date:
1823
Catalogue details

Licence: Public Domain Mark

Credit: A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell. Source: Wellcome Collection.

    349/444 (page 313)
    Hence, bda+b'da' = — sin. 9 cos. 9 sin. (p cos. <pd9 + {cos. 9 cos. <p + sin.2} d<p — {cos. 9 cos.2 (pAr cos. 9 sin.'2 (p} d^p. Also, bda = sin. 9 cos. <p . {cos. 0.sin. <p.d9sin. 9 cos. (pd<p\. Hence, rdt = bda + b'da! + bnda = d(p — cos. 9d\f/. Hence, having found p, q, r, we must determine <p, 9, by means of the equations pdt = sin. (p sin. 9d\p— cos. (pd9 j qdt = cos. (p sin. fldv^ + sin. (pd9>.(*)• -/• dt =d<p — cos. 9 d\]s ' And (p, \p, 9 being known, the position of the body is completely determined. N, N', N, may be functions of (p, \|/. 9. Hence, the six equations (9) and (i), will determine the quantities cp, \p, 9, p, q, r. 126. Prop. A body revolves about its centre of gravity acted upon by no forces; it is required to integrate the equations already found. Take the equations (9), C d r + (B — A) pqdt — Q\ Bdq +(A — C) prdt =0 >.(/c). Adp-\-(C — B) qrdt = OJ Multiply by r, <7, p respectively, and add, and we have Crdr + Bqdq + Apdp = 0 \ Cr2 + £r/ + Ap2 = /*2.(X), h being a constant quantity. Again, multiply equations (/c), by Cr, Bq, and Ap re¬ spectively, and we have C2rdr + B*qdq + A*pdp = 0-, .'. CV -J- B~q~ + A2p2 = lc2, a constant quantity..(m)* R R