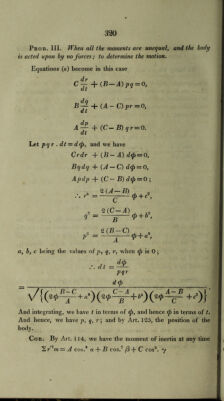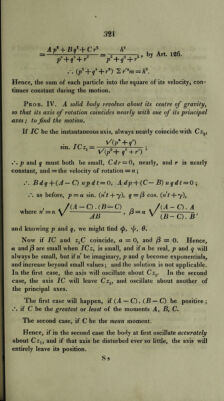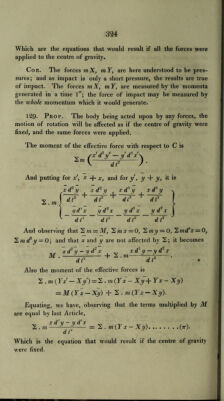A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell.

  • William Whewell
Date:
1823
Catalogue details

Licence: Public Domain Mark

Credit: A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell. Source: Wellcome Collection.

    357/444 (page 321)
    A p* + B q* -\~ C r^ p1 + <f + r~ fi1 V +f + r' , by Art. 126. (/>2 + ?* 4-»*) 2 r'zm — h2. Hence, the sum of each particle into the square of its velocity, con¬ tinues constant during the motion. Prob. IV. A solid body revolves about its centre of gravity, so that its axis of rotation coincides nearly with one of its principal axes; to find the motion. If IC be the instantaneous axis, always nearly coincide with CZj, rn ^(Pz + f) sm. lLz1= ■ - „-—; 1 l/(/+ q+r) p and q must both be small, Cdr = Q, nearly, and r is nearly constant, and = the velocity of rotation = n ; B d q + {A — C) n p d t — 0, A dp -f (C— B) n q d t = 0 ; as before, p = a sin. (n't + y), q—(3 cos. (n't + y), where n' = n (A — C). (B — C) JB (A- a. a (B - C). B ’ and knowing p and q, we might find <p, \]s, 0. Now if IC and zLC coincide, a = 0, and (3 = 0. Hence, a and (3 are small when ICz, is small, and ifn be real, p and q will always be small, but if n be imaginary, p and q become exponentials, and increase beyond small values; and the solution is not applicable. In the first case, the axis will oscillate about Czr In the second case, the axis IC will leave Czv and oscillate about another of the principal axes. The first case will happen, if {A — C). (B — C) be positive ; if C be the greatest or least of the moments A, B, C. The second case, if C be the mean moment. Hence, if in the second case the body at first oscillate accurately about Czt, and if that axis be disturbed ever so little, the axis will entirely leave its position. Ss