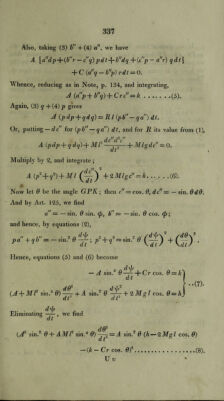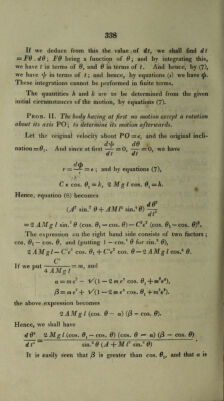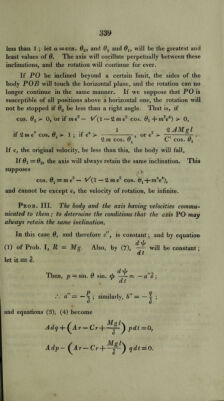A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell.

  • William Whewell
Date:
1823
Catalogue details

Licence: Public Domain Mark

Credit: A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell. Source: Wellcome Collection.

    374/444 (page 338)
    If we deduce from this the value of dt, we shall find dt = F9 . d9 ; F9 being a function of 0; and by integrating this, we have t in terms of 9, and 9 in terms of t. And hence, by (7), we have \]s in terms of t; and hence, by equations (t) we have <p. These integrations cannot be performed in finite terms. The quantities h and k are to be determined from the given initial circumstances of the motion, by equations (7). Prob. II. The body having at first no motion except a rotation about its axis PO; to determine its motion afterwards. Let the original velocity about PO = e, and the original incli- /i , . dd/ d9 nation = 0,. And since at first-= 0, — =0, we have dt dt * d(b . r — —— = e ; and by equations (7), * C e cos. 9i = k, 2 Mg l cos. 91 = h. Hence, equation (8) becomes (A' sin.2 9 +AMT sin.4 9) ~ dt' = 2 AMg I sin.' 9 (cos. 0! —cos. 0) — C2e2 (cos. 0j — cos. 0)2. The expression on the right hand side consists of two factors ; cos. 0X — cos. 0, and (putting 1 — cos.2 0 for sin.2 0), 2 AMgl—CV~ cos. 0i + C V cos. 0 — 2 A Mg l cos.2 0. C2 If we put ——-— — m, and F A AMgl a = tne' — l/(l — 2 m ez cos. 0X + »i2e4), /3 = me~ + V(1 — 2m e2 cos. 0X + m'e*). the above expression becomes 2 AMg l (cos. 0 — a) (/3 — cos. 0). Hence, w^e shall have d 02 2 Mg l (cos. 0X — cos. 0) (cos. 0 — a) (/3 — cos. 0) d T ~ sin.'2 0 {A + M T sin.2 0) It is easily seen that /3 is greater than cos. 9lf and that a is