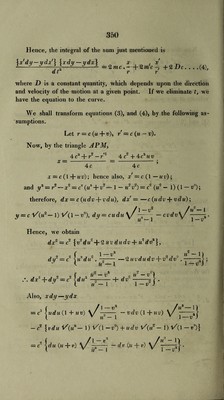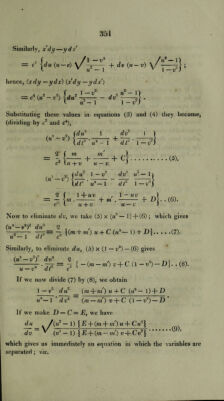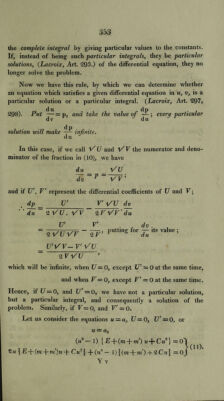A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell.

  • William Whewell
Date:
1823
Catalogue details

Licence: Public Domain Mark

Credit: A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell. Source: Wellcome Collection.

    386/444 (page 350)
    Hence, the integral of the sum just mentioned is {x'dy — ydx'\ \xdy — ydx\ o' , x' _ --^-H—~1 =2»ic.-+2m'c-7 + 2 He. . . dt r r (4), where I) is a constant quantity, which depends upon the direction and velocity of the motion at a given point. If we eliminate t, we have the equation to the curve. We shall transform equations (3), and (4), by the following as¬ sumptions. Let r = c (m + v), r =c (u — v). Now, by the triangle APM, 4 ca + r2-?,,e 4c2+4c*mv x — - = - ; 4 c 4 c or = c (I + mz>); hence also, x=c(l— uv); and y* — r2 — x~ = c' («a + v — 1 — u~ r2) = c~ (u~ — 1) (1 — v1); therefore, dx = c(ydv-\-vdu), dx =—c (ndv + vdu); /]_„2 /M*_i y = c V'(m9 — 1) - Vs), d,U = C«d?f V/ —-— cvdv\f -1 . J J y u — 1 v 1 — X> Hence, we obtain dxq = c~ {v2 dit~-\-2 uvdudv + u dvz}, dij2 = c \u duz . - —2uvdudv-\-vqdv: .-j j; l u-— 1 1 — v ) J 2 , , 2 , j2 »*“«*! dx -{-dy = c —--1- a® -5 f . t u — 1 1 —J Also, xrfy-—yrfx = c1 Iudu (1 + uv) \ f - — vdv (1 -f- uv) \ f-i} ( v u — 1 v 1—v ) — c2 {vdu 1/(«* — 1) 1/(1 — v1) + udv l/(«2 — I) l/(l — O} — C |(/m (?<+«)