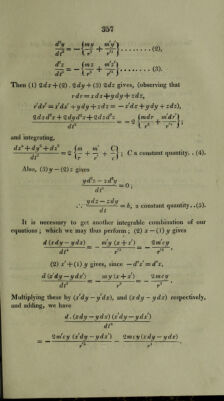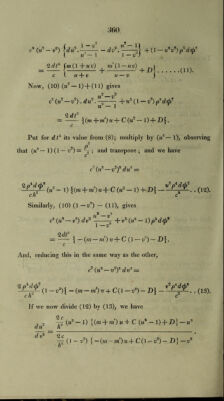A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell.

  • William Whewell
Date:
1823
Catalogue details

Licence: Public Domain Mark

Credit: A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell. Source: Wellcome Collection.

    395/444 (page 359)
    p*d(f> = hdt.(8). To transform equation (6), we may observe that (xdy —ydx) (x'dy—ydx) = xx'dy2 — xdx’.ydy — x dx .ydy-\-y:dxdx\ (xdz — zdx) (x'dz — zdx') = xx'dz~ — x dx'. zdz — x dx . zdz-\- z* dxdx'. And the sum = xx' (dp' 4- p~d<f?) — (xdx 4- x dx) pdp-\-p~dx dx = (xdp — pdx) (xdp — pdx') 4 xx'p1 d(fr. Substituting in equation (6), and multiplying by d t.2, (xdp — pdx) (x'd p — pdx') x x'p' d<p~ , , fmx ni x' 1 = 2cdt* j-1-— + D\.(9). t r r ) We shall now make the same substitution as at p. 350, in the former case, viz., r — c (u 4- v), r = c (u — v). And we shall have the same values of x, x', &c., as we then had, p corresponding to y. Hence, dv2 | vr 'u — 1 1 (xdp- pdx) (x'dp — p dx1) = c4 (u — d2) [du* ~~ — dv* — ~ . I u — 1 1 —v) Substituting these in (7), and (9), observing also that xx' = c~ (1 — ?t2r2); and, dividing the latter by ca, we shall have results analogous to (5) and (6), of the former case, viz., cV—+(?dtf (u — 1 1 — V ) 2 df ( m m \ ]—-1-hCi. . . .(10), IM + W u — v j