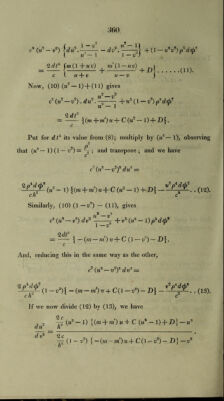A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell.

  • William Whewell
Date:
1823
Catalogue details

Licence: Public Domain Mark

Credit: A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell. Source: Wellcome Collection.

    396/444 (page 360)
    c* (u° — v2) \du~-dv2.-ni + (1—JiV)pd<pf ( u — 1 I — v) <2.dtz (m(\+uv) ^ m’(\—uv) t ^ c l u + v u — v j Now, (10) (if— 1) H- (11) gives 2_ 2 c (if — v~). d if. —-f- id (1 — v~) a d <p~ u~ — 1 O flf- = - { (m + m) u-t C (if — 1) -+- D }. c Put for dt3 its value from (8); multiply by (id— l), observing © that (id — 1) (1 — v2) = ; and transpose; and we have (12). 2/2 2\2 J 2 c (?/ — v j du == 2/0 (if - 1) \(m-)rm)u-\- C (id — l) -f D] — - P f^ . . ch~ c Similarly, (10) (1 — v2) — (11), gives c2 (if1 - V*) dv* ^ + V% (id - 1) p*d(p* Qdf- — - { — (m — m) v + C(l — v') — D}. c And, reducing this in the same way as the other, c~ (id — v2)2 did — -p d(j) ^ —v2)[ — (m — m')v + C(l—v*) — D] — -■? . . (13). c If r If we now divide (12) by (13), we have C) /> did Id ~ ^ i(m + ”*')u + C (u1 - l) + D} — id yj (1 — v~) { ~(m — m')u + C(l — vz) — D} — id