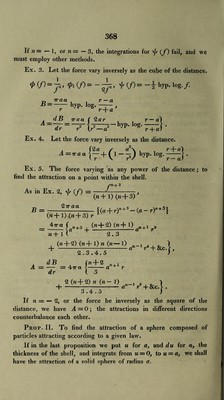A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell.

  • William Whewell
Date:
1823
Catalogue details

Licence: Public Domain Mark

Credit: A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell. Source: Wellcome Collection.

    404/444 (page 368)
    If n = — 1, or 11= — 3, the integrations for \{s (f) fail, and we must employ other methods. Ex. 3. Let the force vary inversely as the cube of the distance. <p(f)=j3> (f>= 0 (/)= ~i hyp-log-/- Tract r-a —- hyp. log. r + a 3 dB ir a a ( 2a r r—a\ A=Tr=T Iw - hJP- —J ■ Ex. 4. Let the force vary inversely as the distance. . (2a / a2\ , , r + a} A=*aa\-+(l--) hyp. log.—}. Ex. 5. The force varying as any power of the distance; to find the attraction on a point within the shell. fn+ 3 As in Ex. 2, \ls (f) =----, Y J (n + 1) (;t + 3) 3 B = 2iraa (»+l) (« + 3) r 47ra f _ = -\a n + 1 l {(a + r)n + 3-(a-r)n+3\ + 3 , (”+g) <” + l2 an +1 2.3 + dB (n + 2) 0+ 0 n (n— l) x -_—. a dB ( =- = 4tt a { dr \ 2.3.4.5 ?i + 2 r4 + &c }. _« +1 a r 2 (n + 2) n (n — ]) . , + -A -1-- a 1 r3 + &c, 3.4.5 }• If n = — 2, or the force be inversely as the square of the distance, we have A = 0; the attractions in different directions counterbalance each other. Prop. II. To find the attraction of a sphere composed of particles attracting according to a given law. If in the last proposition we put u for a, and du for a, the thickness of the shell, and integrate from u = 0, to u = a, we shall have the attraction of a solid sphere of radius a.