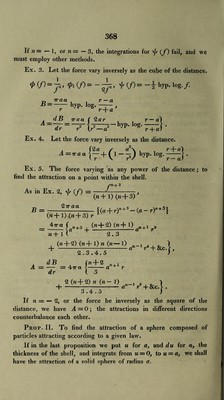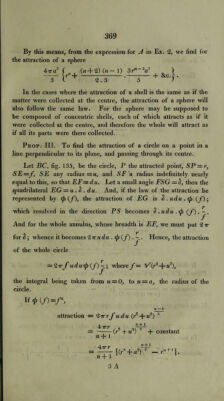A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell.

  • William Whewell
Date:
1823
Catalogue details

Licence: Public Domain Mark

Credit: A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell. Source: Wellcome Collection.

    406/444 (page 370)
    Ex. 1. Let n = — 2, or the force vary inversely as the square of the distance. Here, attraction = 4tv 11 — ■ . --s-i . X V (r + o3)J Ex. 2. Let the circle be infinite, and n < — 1. n + 1 In this case (r2 + a2) 2 becomes 0, and we have, putting — m for n, Air attraction = -- . (m— 1) r * If w = 2, attraction = 47r, and is the same at all distances. Prop. IV. To find the attraction of a solid of revolution on a point in the axis. We must here multiply the attraction of the circle, found in the last Proposition, by the thickness dr, for the attraction of a differential slice; and if we then put for a its value in terms of r, and integrate, we have the attraction of the whole solid. Ex. 1. The attraction of a cylinder on a point in its axis; fig. 136. 47T attraction =- C \rdr (r3, + a2) n+ 1 J 1 »+ \ ,2\ 2 — ? ,n+ 2, d?'} n -4* 3 4 7r | (r2 4- a2) n + 1 1 n -M + 3 + constant! ! -J- 3 n -f- 3 If BSC and B'S'C1 be the two ends of the cylinder, and if PS = b, PS' = b\ PC = c, PC' = c, we have attraction = —■ ■*”'-- {c'n+3 — c”+3— (b'n + 3— 6,,l + 3)}. (« + ])(w + 3)1 If the force vary inversely as the square of the distance, n = — 2, attraction = 47r {b' — b — (c —c)}. Ex. 2. The attraction of an infinite solid bounded by planes. In last Prop. Ex. 2, multiply by dr, and we have 47t /* dr 47t attraction 47t dr = m- 1 J {m — 1) (m -3){bm-3 r™-^’