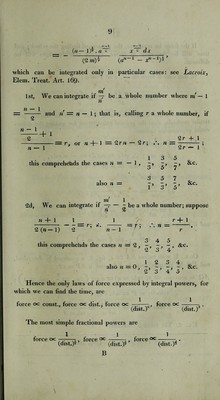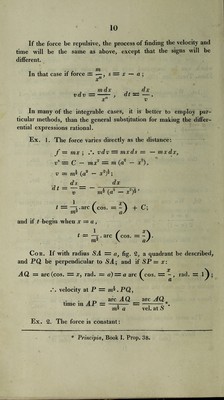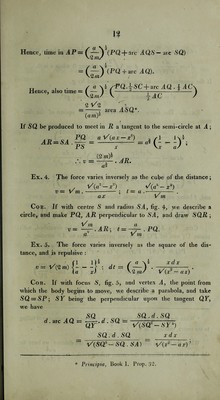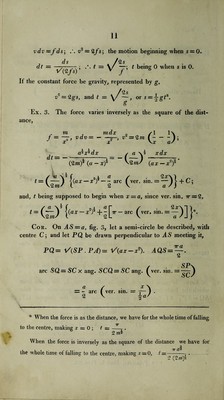A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell.

  • William Whewell
Date:
1823
Catalogue details

Licence: Public Domain Mark

Credit: A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell. Source: Wellcome Collection.

    48/444 (page 12)
    vdv=zfds; u* 2 = 2fs-, the motion beginning when s = 0. ds /2s dt = t — v t being 0 when s is 0. If the constant force be gravity, represented by g, /os v' = 2gs, and t — \/—, or s = ^gt*. or <5 Ex. 3. The force varies inversely as the square of the dist¬ ance, m max /I lx J = ~, vdv=-—, it = 2 w (-1; x x \x as a^x^dx / a \i xdx (2wi)^ (a — x)2 \2ms (ax — x2)^ ver. sin -7>)*<=‘ and, t being supposed to begin when x — a, since ver. sin. 7t = 2, t=(Ly (''er-si-=if)]}'- Cor. On AS = a, fig. 3, let a semi-circle be described, with centre C; and let PQ be drawn perpendicular to AS meeting it, PQ= V(SP .PA)= V(ax-x*). AQS = —-. 2 arc SQ = SCx ang. SCQ—SC ang. ^ver. sin. = a s x\ = - arc ( ver. sm. = — 1 . 2 V * When the force is as the distance, we have for the whole time of falling to the centre, making x = 0 ; t = —. 2 m* When the force is inversely as the square of the distance we have for 7T fll the whole time of falling to the centre, making .r = 0, t =-—- . 2(2 ?n)i