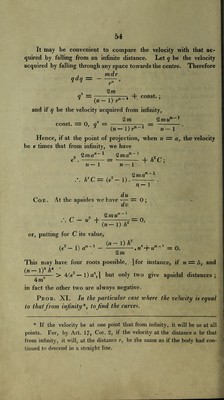A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell.

  • William Whewell
Date:
1823
Catalogue details

Licence: Public Domain Mark

Credit: A treatise on dynamics. Containing a considerable collection of mechanical problems / By William Whewell. Source: Wellcome Collection.

    90/444 (page 54)
    It may be convenient to compare the velocity with that ac¬ quired by falling from an infinite distance. Let q be the velocity acquired by falling through any space towards the centre. Therefore 7 mdr qdq — - r 2m —i + const.; (n- 1) r11 and if q be the velocity acquired from infinity, „ 2m 2mun~* const. = 0, q — (n — 1) r‘ ,71 — 1 1 Hence, if at the point of projection, when u = a, the velocity be e times that from infinity, we have 2m a 71—1 2 rn a n- i 71— 1 n — 1 + h*C; h'C = (e2 — 1) 2 m a n-i n— i du Cor. At the apsides we have — = 0 ; dv .-. c - «2 + 2 771U n- 1 (n — 1) h 7=0, or, putting for C its value, (e2— 1)0-' - + =0. 2m This may have four roots possible, {for instance, if n — 5, and _])* * --— > 4(e2—l)a4,} but only two give apsidal distances; 4 m in fact the other two are always negative. Prob. XI. hi the 'particular case where the velocity is equal to that from injinity*, to find the curves. * If the velocity be at one point that from infinity, it will be so at all points. For, by Art. 17, Cor. 2, if the velocity at the distance a be that from infinity, it will, at the distance r, be the same as if the body had con¬ tinued to descend in a straight line.