The microscope and its revelations / by the late William B. Carpenter.

  • William Benjamin Carpenter
Date:
1891
Catalogue details

Licence: Public Domain Mark

Credit: The microscope and its revelations / by the late William B. Carpenter. Source: Wellcome Collection.

Provider: This material has been provided by The University of Leeds Library. The original may be consulted at The University of Leeds Library.

    83/1184 (page 55)
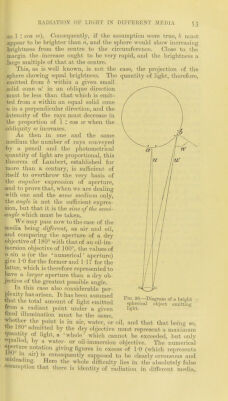
    A dry objective was therefore supposed to be placed at a disad- vantage when used upon balsam-mounted objects, its aperture being supposed to be ' cut down' by the balsam, and the advantage of the immersion objective was considered to rest on the fact that it restored, in the case of the balsam-mounted object, the same condi- tions as subsisted in the case of the dry-mounted object, allowing as large (but no larger) an aperture to be obtained with the former object as is obtained by the dry objective with the latter. ' The error here lies in the assumption of the identity of radiation in air and balsam. If there were in fact any such identity, the 170° IN AIR BALSAM 1 Fig. 38. conclusion above referred to would, of coursCj be correct, for if in tig. 37 the ah- pencil of 170° was identical with the balsam pencil of 170° (shown by the dotted lines in tig. 38), there would necessarily he a relative loss of light in the latter case in consequence of so- much of the pencil being reflected back at the cover-glass. When, however, the increase of radiation with the increase in, the refractive index of the medium is recognised, the mistake of the preceding view is appreciated. The 170° in air of fig. 37 is not equal to, but much less than, the 170° in balsam of iig. 38, and not- withstanding that a great part of the latter does not reach the proportion of the squares of tlieir radii, it follows that if we designate the radius by n sin u (or ;u sin (p), the area of the circle A will be to the area of the circle B as the square of the radius of A is to the square of the radius of B, or as {n sin u)- is to- («' sin u']'^, B Ai'eco -proportf.onal to (ih'sirv iv)'^ Area- j)7^opoTtio/iaZ to (jU/ sirh ^j-? Pre. A 2.—The backs of two objectives of the same power but diiTereiit apertures. The student will observe that the radius of B is twice that of the radius of A; consequently the area of B will bo four times as great ns that of A; which moans that, since the numerical aperture of the objective B is twice as great as that of tho objective A, its illuminating power will be four times as great.