Oeuvres ophthalmologiques de Thomas Young / traduites et annotées par M. Tscherning ; précédées du portrait de Young, de son éloge par François Arago et d'une préface par Émile Javal.

Thomas Young

Date:: 1894

Credit: Oeuvres ophthalmologiques de Thomas Young / traduites et annotées par M. Tscherning ; précédées du portrait de Young, de son éloge par François Arago et d'une préface par Émile Javal. Source: Wellcome Collection.

Provider: This material has been provided by the Francis A. Countway Library of Medicine, through the Medical Heritage Library. The original may be consulted at the Francis A. Countway Library of Medicine, Harvard Medical School.

98/274 (page 82)

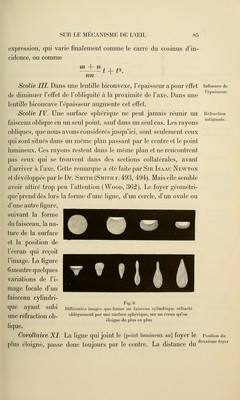
$Réfraction à in- cidence oblique Proposition IV. Théorème Lorsque le rayon incident rencontre obliquement une sur- face sphérique, la droite (AI, KL) qui joint deux foyers con- jugués (A, I; K, L) passe au point d'intersection (G) de la ligne (EF) bissectrice des deux cordes (BC, BD), découpées [par la surface] dans les rayons incident et réfracté — et de la perpendiculaire abaissée du centre (H) sur cette ligne. sur une surface sphérique et sur une sur- face plane. Distance focale principale. La caustique est limitée. Fig.5 Corollaire I Désignons par t et u les cosinus des angles d'in- cidence et de réfraction, par d et e les distances respectives des foyers du rayon incident [l'objet] et du rayon réfracté [l'image], et prenons le rayon de la surface comme unité. On a alors mduu mdu — ndt — ntt Corollaire IL Pour une surface plane on obtient l'expression mduu — ntt Corollaire III. Pour des rayons parallèles on a d = <x> muu mu — nt Scolie I. Il est à remarquer que la caustique de réfraction, si on la considère d'un point de vue physique et non géométrique, finit près du sommet, parce que la réflexion totale intervient. Corollaire IV. Mettons muu mu—nt = b$