On the sensations of tone as a physiological basis for the theory of music / by Hermann L.F. Helmholtz ; translated, thoroughly revised and corrected, rendered conformable to the 4th (and last) German edition of 1877, with numerous additional notes and a new additional appendix bringing down information to 1885, and especially adapted to the use of musical students, by Alexander J. Ellis.
- Hermann von Helmholtz
- Date:
- 1895
Licence: Public Domain Mark
Credit: On the sensations of tone as a physiological basis for the theory of music / by Hermann L.F. Helmholtz ; translated, thoroughly revised and corrected, rendered conformable to the 4th (and last) German edition of 1877, with numerous additional notes and a new additional appendix bringing down information to 1885, and especially adapted to the use of musical students, by Alexander J. Ellis. Source: Wellcome Collection.
47/604 (page 23)
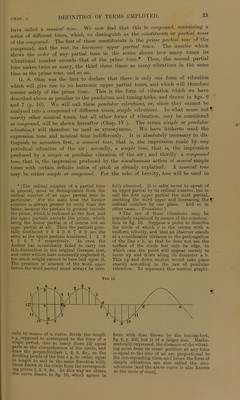
![DEFINITION OF TERMS EMPLOYED. have called a musical tone. Wc now find that this is compound, containing a scries of different tones, which we distinguish as the constituents or partial tones 0f the compound. The first of these constituents is the prime partial tone of the compound, and the rest its harmonic upper partial tones. The number which shows the order of any partial tone in the series shows how many times its vibrational number exceeds that of the prime tone.* Thus, the second partial tone makes twice as many, the third three times as many vibrations in the same time as the prime tone, and so on. G. S. Ohm was the first to declarc that there is only one form of Vibration which will give rise to no harmonic upper partial tones, and which will therefore consist solely of the prime tone. This is the form of Vibration which we have dcscribed above as peculiar to the pendulum and tuning-forks, and drawn in figs. G and 7 (p. 10). We will call these pendular vibrations, or, since they cannot be analysed into a compound of different tones, simple vibrations. In what sense not rnerely other musical tones, but all other forms of Vibration, may be considered as compound, will be sliown hereafter (Chap. IV.). The terms simple or pendular Vibration,t will therefore be used as synonymous. We have hitherto used the expression tone and musical tone indifferently. It is absolutely necessary to dis- tinguish in acoustics first, a musical tone, that is, the impression made by any periodical Vibration of the air; secondly, a simple tone, that is, the impression produced by a simple or pendular Vibration of the air; and thirdly a compound tone, that is, the impression produced by the simultaneous action of several simple tones with certain definite ratios of pitch as already explained. A musical tone may be either simple or compound. For the sake of brevity, tone will be used in * [The ordinal number of a partial tone in general, must be distinguished from the ordinal number of an upper partial tone in particular. For the same tone the former number is always greater by unity than the latter, because the partials in general include the prime, which is reckoned as the first, and the upper partials exclude the prime, which being the loxocst partial is of course not an upper partial at all. Thus the partials gene- rally numbered 23456789 are the same as the upper partials numbered 12 3 4 5 6 7 8 respectively. As even the Author has occasionally failed to carry out this distinction in the original German text, and other writers have constantly neglected it, too much weight cannot be here laid upon it. The presence or absence of the Word upper before the word partial must always be care- fully observed. It is safer never to speak of an upper partial by its ordinal number, but to call the fifth upper partial the sixth partial, omitting the word upper and increasing the 51 ordinal number by one place. And so in other cases.—Translator.'] t The law of these vibrations may be popularly explained by means of the construc- tion in fig. 10. Suppose a point to describe the circle of which c is the centre with a uniform velocity, and that an observer Stands at a considerable distance in the Prolongation of the line e h, so that he does not see the surface of the circle but only its edge, in which case the point will appear rnerely to move up and down along its diameter a b. This up and down rnotion would take place exactly according to the law of pendular Vibration. To represent this rnotion graphi- Fm. 10. cally by means of a curve, divide the length e K> supposed to correspond to the time of a single period, into as many (here 12) equal parts as the circumfercnce of the circle, and draw the perpendiculars 1, 2, 3, &c., on the dividmg points of the line e g, in order, equal in length to and in the same direction with, tnose drawn in the circle from the correspond- mg points 1, 2, 3, &c. In this way wo obtain the curve drawn in fig. 10, which agrees in form with that drawn by the tuning-fork, fig. 6, p. 206, but is of a larger size. Mathe- matically oxpressed, the distance of the vibrat- ing point from its mean position at any time is equal to the sine of an arc proportional to the corresponding time, and henco the form of simple vibrations are also called the sine- vibrations [and the above curve is also known as the curve of sincs].](https://iiif.wellcomecollection.org/image/b28141532_0047.jp2/full/800%2C/0/default.jpg)