On the sensations of tone as a physiological basis for the theory of music / by Hermann L.F. Helmholtz ; translated, thoroughly revised and corrected, rendered conformable to the 4th (and last) German edition of 1877, with numerous additional notes and a new additional appendix bringing down information to 1885, and especially adapted to the use of musical students, by Alexander J. Ellis.
- Hermann von Helmholtz
- Date:
- 1895
Licence: Public Domain Mark
Credit: On the sensations of tone as a physiological basis for the theory of music / by Hermann L.F. Helmholtz ; translated, thoroughly revised and corrected, rendered conformable to the 4th (and last) German edition of 1877, with numerous additional notes and a new additional appendix bringing down information to 1885, and especially adapted to the use of musical students, by Alexander J. Ellis. Source: Wellcome Collection.
51/604 (page 27)
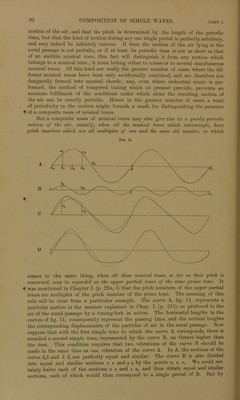
![And yet, as the ear is able to distinguish all the separate constituent parts of this confused whole, \ve are forced to conclude that all these different Systems of wave coexist in the mass of air, and leave one another mutnally undistnrbed. But how is it possible for them to coexist, since every individual train of waves has at any particular point in the mass of air its own particnlar degree of condensa- tion and rarefaction, which determines the velocity of the particles of air to this side or that 1 It is evident that at each point in the mass of air, at each instant of time, there can be only one single degree of condensation, and that the particles of air can be moving with only one single determinate kind of motion, having only one single determinate amount of velocity, and passing in only one single deter- minate direction. What happens ander such circumstances is seen directly by the eye in the waves of water. If where the water shows large waves we throw a stone in, the waves thus caused will, so to speak, cut into the larger moving surface, and this U surface will be partly raised, and pavtly depressed, by the new waves, in such a way that the fresh crests of the rings will rise just as much above, and the troughs sink just as much below the curved surfaces of the previous larger waves, as they would liave risen above or sunk below the horizontal surface of calm water. Hence where a crest of the smaller System of rings of waves comes upon a crest of the greater System of waves, the surface of the water is raised by the sum of the two heights, and where a trough of the former coincides with a trough of the latter, the surface is depressed by the sum of the two depths. This may be expressed more briefly if we consider the heights of the crests above the level of the surface at rest, as positive magnitudes, and the depths of the troughs as negative magnitudes, and then form the so-called algebraical sum of these positive and negative magnitudes, in which case, as is well known, two positive magnitudes (heights of crests) must be added, and similarly for two negative magnitudes (depths of troughs); but when both negative and positive concur, one is to be subtracted U from the otlier. Performing the addition then in this algebraical sense, we can express our description of the surface of the water on which two Systems of waves concur, in the following simple mann er.: The distance of the surface of the water at any point from its position of rest is at any moment equal to the [algebraical] sum of the distances at ivhich it ivould have stood had each ivave acted separately at the same place and at the same time. The eye most clearly and easily distinguislies the action in such a case as has been just adduced, where a smaller circular System of waves is produced on a large rectilinear System, because the two Systems are then strongly distinguished from each other both by the height and shape of the waves. But with a little attention the eye recognises the same fact even when the two Systems of waves have but slightly different forms, as when, for example, long rectilinear waves advancing towards the sliore concur with those reflccted from it in a slightly different direction. In this case we observe those well-known comb-backed waves where U the crest of one System of waves is heightened at sorne points by the crests of the other System, and at others depressed by its troughs. The multiplicity of forms is here extremely great, and any attempt to describe them would lead us too far. 1 he attentive observer will readily comprehend the result by examining any disturbed surface of water, without further description. It will suffice for our purpose if the first example has given the reader a clear conception of what is meant by adding waves toyether.* Hence although the surface of the water at any instant of time can assume only one single form, while each of two different Systems of waves simultaneously attempts to impress its own shape upon it, we are able to suppose in the above Ihe velocities and displacemonts of the particles of water are also to be added accord- ing to the law of the so-called parallelogram O forces. Strictly speaking, such a simple addition of waves as is spoken of in the text, is not perfectly correct, unless the heights of the waves are infinitely small in comparison with their lengths.](https://iiif.wellcomecollection.org/image/b28141532_0051.jp2/full/800%2C/0/default.jpg)