Physiologic optics : dioptrics of the eye, functions of the retina, ocular movements and binocular vision / by M. Tscherning ; authorized translation from the original French edition., specially revised and enlarged by the author by Carl Weiland.

  • Marius Tscherning
Date:
1904
Catalogue details

Licence: In copyright

Credit: Physiologic optics : dioptrics of the eye, functions of the retina, ocular movements and binocular vision / by M. Tscherning ; authorized translation from the original French edition., specially revised and enlarged by the author by Carl Weiland. Source: Wellcome Collection.

Provider: This material has been provided by The University of Glasgow Library. The original may be consulted at The University of Glasgow Library.

    33/392 (page 5)
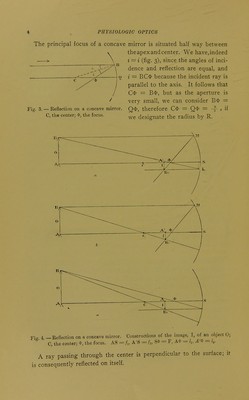
    Construction of the Image. — To find the image of a point B (fig. 4), it suffices to trace the course of two rays which have emanated from that point; the image must be at the place where they intersect after reflection. After what has been previously stated we 'already know the course of three rays proceeding from the point B. 1°. The ray BM, which is parallel to the axis, passes after reflection through the focus *; 2°. The ray B4>, which passes through the focus, is reflected parallel to the axis since the course of the rays is reversible; 3°, The ray BC, passing through the center, is reflected on itself. Two of these rays suffice for the construction. By combining them, two by two, we obtain the three different constructions shown in figure 4. Size of the Image. Relations Between the Distances of Con- jugate Points.—Let us consider the line BA = O (fig. 40) as the object; I is its image. And supposing SL = I and MS = O, the triangles AB* and SL^' on one side, and the triangles SM^* and A'B'4> on the other give us the relations The formula ^ = = Z or /i ?2 = FF i^^wtony 1 F L = -1 can also be written — = —' IF I R which is the formula we use later in ophthalmometry. — As we have l^ = f^ — F and ^2 = ^2 — F, the formula of Newton h h = FF can also be written F , F , 1 , 1 _ 1 The first of these two formulae is that of Hclmholts; and, as we shall see, it is altogether general. The second is identical with that of infinitely thin lenses. (1) In this formula and those which follow I designate by: 0, the object; 1, the image; R,, the radius of the first surface; R2, the radius of the second surface; F], the anterior focal distance; Fj, the pofterior focal distance; /■], the distance of the object from the surface; fi, the distance of the image from the surface; I], the distance of the object from the anterior focus; ^2, the distance of the image from the posterior focus; For mirrors and lenses surrounded with the same media on both sides we have Fi — Fj = F t