Treatise on natural philosophy : Vol 1. Part 2 / by Sir William Thomson and Peter Guthrie Tait.
- Date:
- 1883
Licence: Public Domain Mark
Credit: Treatise on natural philosophy : Vol 1. Part 2 / by Sir William Thomson and Peter Guthrie Tait. Source: Wellcome Collection.
Provider: This material has been provided by the Royal College of Physicians of Edinburgh. The original may be consulted at the Royal College of Physicians of Edinburgh.
489/594 page 459
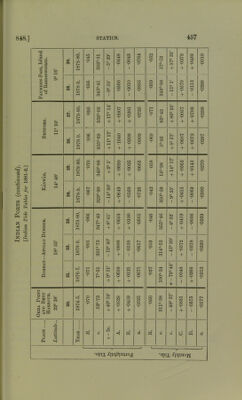
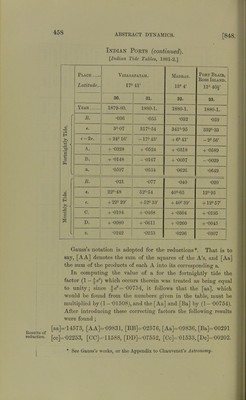
![Then according to the method of least squares, the following the most probable values of x, y, u, v. are Results of reduction. _ [Aa] “ [aa] ’ y“[aa]’ [co] ’ v = [Dc] [cc]* And if m be the number of observations (which in the present case is 33) the mean errors of x, y, u, v are respectively 1 /[AA] [aa] — [Aa]: [aa] V 7/i-l 1 /[CC] [cc]-[CcJ2 [cc]V vi-l ’ 1 /[BB] [aa] - [Ba]3 [aa] V in - 1 1_ /[DD][cc] - [Dc]2 [cc] 'V m— 1 The probable errors are found from the mean errors by multi- plying by ‘6745. I thus find that x — ‘675 + -056, y = -020 ± '055, u = -680 + -258, v = -090 ± -218. The smallness of the values of y and v is satisfactory; for, as stated above (§ 848 (d)), if the equilibrium theory were true for the two tides under discussion, they should vanish. Moreover the signs are in agreement with what they should be, if friction be a sensible cause of tidal retardation. But considering the magnitude of the probable errors, it is of course rather more likely that the non-evanescence of y and v is due to errors of observation*. If the solid earth does not yield tidally, and if the equi- librium theory is fulfilled, x and u should each be approximately * Shortly after these computations were completed Professor Adams hap- pened to observe a misprint in the Tidal Report for 1872. This Report gives the method employed in the reduction by harmonic analysis of the tidal obser- vations, and the erroneous formula relates to the reduction of the tides of long period. On inquiring of Mr Roberts, who has superintended the harmonic analysis, it appears that the erroneous formula has been throughout used in the reductions. A discussion of this mistake and of its effects will be found in a paper communicated to the British Association by me in 1882. It appears that the values of the fortnightly tide are not seriously vitiated, but the monthly elliptic tide will have suffered much more. This will probably account for the large probable error which I have found for the value of the monthly tide. If a recomputation of all the long-period tides should be carried out, I think there is good hope that the probable error of the value of the fortnightly tide may also be reduced.](https://iiif.wellcomecollection.org/image/b21987312_0489.jp2/full/800%2C/0/default.jpg)